UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 1.1a
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Passo 1
Fala aí pessoal, tudo bem com vocês?
Nessa questão recebemos duas curvas:
E, precisamos primeiro esboçar a região entre essas curvas. E, depois, calcular a área dessa região.
Para isso, vamos começar relembrando o gráfico das curvas dadas, e depois encontramos os pontos de intersecção pra delimitar direitinho a região dada.
Pra calcular a área, podemos usar as queridas integrais, usando que:
onde é justamente as curvas que determinam essa área superiormente e inferiormente.
Tranquilo?! Então vamos nessa!
Passo 2
Bom, vamos começar pela reta . É uma reta que passa pela origem, e tem inclinação de :
Já o gráfico da curva:
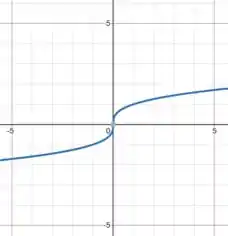
Como esses gráficos são de funções fundamentais, é importante conhecermos os seus formatos, beleza?
Agora vamos plotar ambos as curvas em um mesmo gráfico:
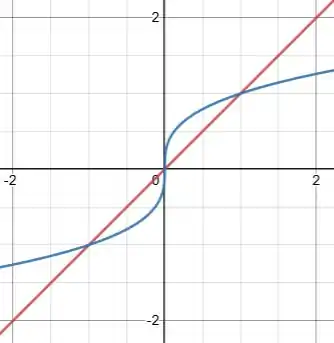
Temos uma região delimitada pelas curvas que está acima do eixo e outa abaixo. Vamos calcular a área de cada uma delas e somar.
Se a gente olhar direitinho, temos pontos de intersecção. Vamos calculá-los. Para isso, igualamos as equações:
Além disso, elevando ao cubo em ambos os lados:
Temos a solução trivial:
Daí, dividindo por dos dois lados:
Portanto, temos três pontos de intersecção:
Massa! Sabendo disso vamos calcular a área 😊
Passo 3
Para calcular a área, vamos utilizar a integral que comentamos no passo .
No intervalo de a , a função vai por cima de , ou seja, é maior do que essa última.
Daí, podemos fazer:
Logo:
A área da região que está acima do eixo é calculada da mesma forma, porém agora a função é maior do que . Assim:
Logo:
Sendo assim, a área dessas regiões vale:
Portanto:
E aí galera, curtiram a solução? Responde Aí!