UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 1.1f
Esboce a região limitada pelas curvas indicadas e encontre sua área:
Passo 1
E aí pessoal, tudo certo?
Nessa questão recebemos duas curvas:
E, precisamos primeiro esboçar a região entre essas curvas. E, depois, calcular a área dessa região.
Para isso, vamos começar relembrando o gráfico das curvas dadas, e depois encontramos os pontos de intersecção pra delimitar direitinho a região dada.
Pra calcular a área, podemos usar as queridas integrais, usando que:
onde é justamente as curvas que determinam essa área superiormente e inferiormente.
Tranquilo?! Então vamos nessa!
Passo 2
Bom, vamos começar esboçando a curva:
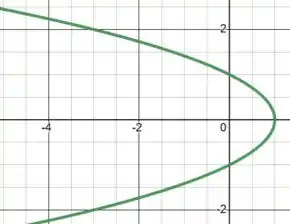
Já para:
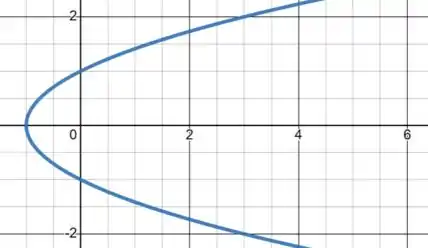
Juntando ambas as curvas em um mesmo gráfico, temos:
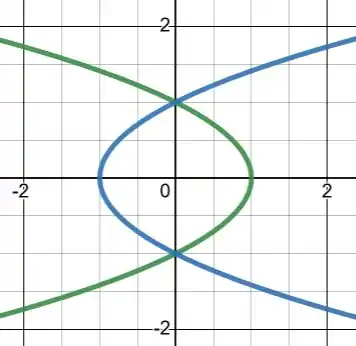
Assim, a região delimitada entre as curvas está justamente entre os pontos que as curvas tocam o eixo , ou seja .
Passo 3
Para calcular a área, vamos utilizar a integral que comentamos no passo .
Porém, iremos considerar como sendo a reta .
Assim, de a , vem:
Logo, como a outra parte, limitada pela curva é simétrica a essa, temos:
Prontinhooo! Obrigado pela atenção pessoal 😊