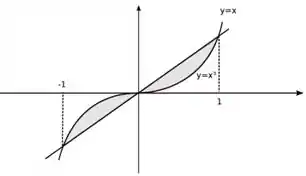
Esboce a região limitada pelas curvas e e em seguida calcule a área desta região.
Passo 1
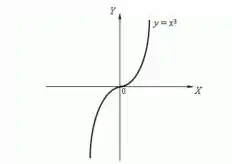
Sabemos que o gráfico de é uma reta crescente que passa pela origem. Já o gráfico de tem a seguinte forma
A área limitada por esses dois gráficos, portanto, é:
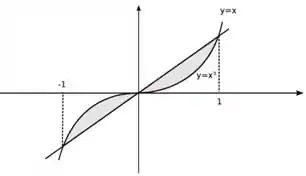
Passo 2
Os pontos de interseção das curvas são:
Portanto teremos que integrar nos intervalos e para descobrir a área desejada. Observe que, no intervalo , , logo, a integral que representa a área delimitada pelas curvas nesse intervalo é:
Já no intervalo, , portanto a integral que representa a área nesse intervalo é:
A área total é a soma dessas integrais:
Resposta