- Esboce a região do plano delimitada pela parábola , pela reta e pelo eixo .
- Calcule o valor da área da região .
Passo 1
(a)
Bom, aqui a princípio nenhuma grande dificuldade, só temos que esboçar uma parábola e uma reta.
A essa altura do campeonato, já estamos carecas de ver a parábola :
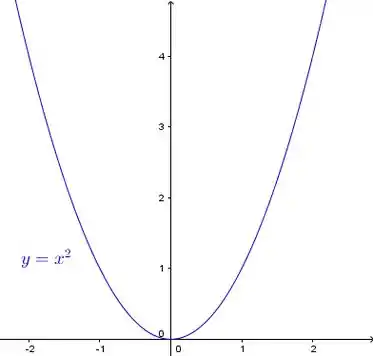
Passo 2
E pra esboçar a reta podemos ver onde ela cruza os eixos coordenados:
Portanto a reta passa pelos pontos e .
Aqui está ela:
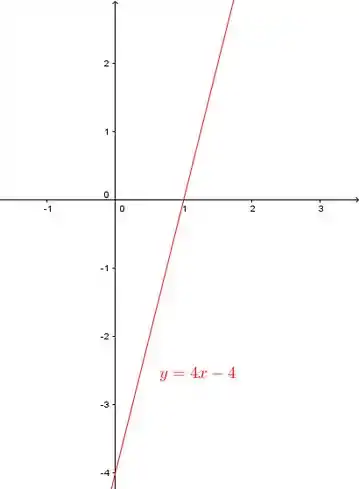
Passo 3
A região é limitada pela parábola, pela reta e pelo eixo , então ela vai ser assim:
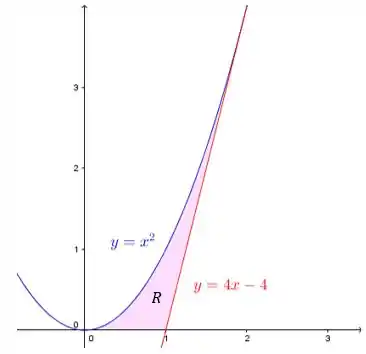
Passo 4
(b)
Pela figura deu pra ver que a parábola e a reta se interceptam em um ponto, então vamos achar que ponto é esse!
Igualando as equações das curvas
Repare que isso dá:
Beleza, então as curvas se interceptam em .
Passo 5
Agora já podemos montar a integral pra calcular a área. Na verdade, vão ser duas integrais.
Com , quem está limitando a região é a parábola (em cima) e o eixo (embaixo).
Com , a região está entre a parábola (em cima) e a reta (embaixo).
Então a área da região vai ser:
Passo 6
Show, agora é só integrar! :)
A primeira integral é:
E a segunda:
Juntando as duas, a área vai dar:
Resposta
(a)
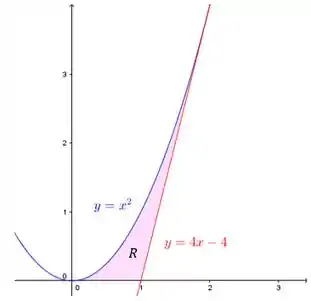
(b)