Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 229123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre Curvas

Na figura abaixo está o gráfico de g x = 1 1 + x 2 .

Seja f x = 1 - x 2 2 . Desenhe a região compreendida entre os gráficos de f e g e as retas x = 0 e x = 2 . Calcule a sua área.

Passo 1

Bom, basta que desenhemos a parábola em cima do desenho já dado. Sabemos que ela tem boca para baixo e que cruza o eixo y em y = 1 . Basta que analisemos suas raízes e interseções com o gráfico dado:

1 - x 2 2 = 0 → x = ± 2   ( R a í z e s   d a   p a r á b o l a )

1 - x 2 2 = 1 1 + x 2 → 2 - x 2 2 = 1 1 + x 2

2 = 2 + x 2 - x 4

x 4 = x 2

x = 0   ; x = ± 1   ( I n t e r s e ç õ e s   c o m   g ( x ) )

Aí é só esboçar e marcar a área do gráfico entre x = 0 e x = 2 compreendida entre os dois gráficos:

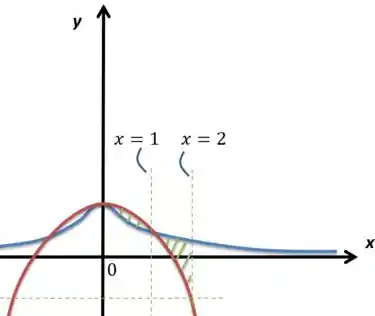
O que está marcado em verde é a área entre os gráficos. Agora basta que integremos as áreas, com o detalhe que entre 0 e 1 temos o vermelho por cima e daí até o 2 ele vai por baixo. Fica assim nossa integral:

A = ∫ 0 1 f x - g x d x + ∫ 1 2 g x - f x d x

= ∫ 0 1 1 - x 2 2 - 1 1 + x 2 d x + ∫ 1 2 1 1 + x 2 - 1 + x 2 2 d x

= x - x 3 6 - arctg ⁡ x [ 1 0 + arctg ⁡ x - x + x 3 6 [ 2 1

= 1 - 1 6 - arctg ⁡ 1 - 0 - 0 6 - arctg ⁡ 0 + arctg ⁡ 2 - 2 + 8 6 - arctg ⁡ 1 - 1 + 1 6

= 5 6 - π 4 - 0 + arctg ⁡ 2 - 2 3 - π 4 - 5 6 = 1 - π 2 + arctg ⁡ ( 2 )

Resposta

A = 1 - π 2 + arctg ⁡ ( 2 )

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x