UFU, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Trabalho C1 - 2022.1, Questão 5ab.
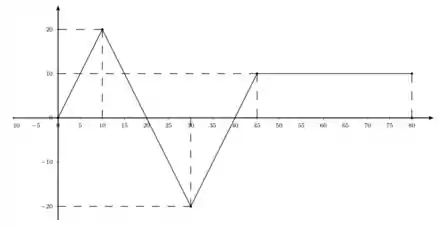
5. A figura 1 representa o gráfico de uma função definida no intervalo . Calcule as integrais abaixo:
a)
b)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nessa questão queremos obter algumas integrais de dentro de alguns intervalos.
Mas sem como podemos obter esses resultados? 🤔
Pra isso foi dado um gráfico de no intervalo .
Pra resolver esse problema temos que lembrar de uma definição das integrais. Ao integrar uma função dentro de um intervalo, estamos calculando a área abaixo dessa função desse intervalo.
Sacou? Bora começar! 😁
Passo 2
Para a primeira integral, temos que obter , ou seja, a área abaixo de entre e .
O gráfico de é dado por
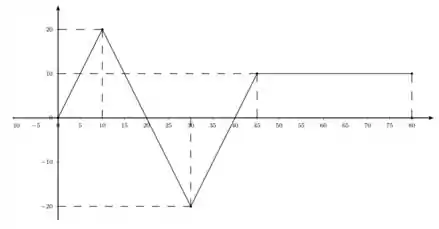
Entre e , a figura que se forma é um triângulo de base e altura . Ou seja, se a área de um triangulo é dado por
Tranquilo até aqui? 😉
Passo 3
Agora para a integral , perceba que a figura que se forma entre e o eixo é outro triangulo de base e altura ...
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
a)
b)