UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Matheus Nunes - Lista 7, Questão 8k
Final. 2011.2 Seja Encontre a área da região delimitada pelo gráfico de , pelo eixo e pelas retas e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para encontrar a ��rea da região delimitada pelo gráfico de , pelo eixo e pelas retas e .
Plotando primeiramente o gráfico com os dados fornecidos na questão, temos:
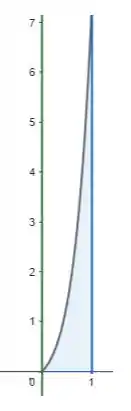
Para descobrir a área da região, basta fazermos a integral da função no intervalo !!
E aí?? Bora lá??
Passo 2
Aplicando a função , temos:
Fazendo , temos:
Aplicando a integral por partes, temos:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x