O gráfico de consiste de dois segmentos de retas e um semi-circulo, conforme a figura abaixo.
Calcule:
a)
b)
c)
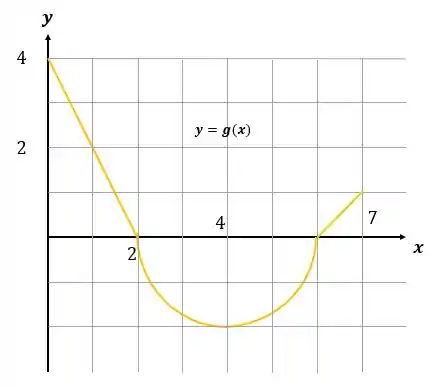
Passo 1
Fala aí, galera! Vamos fazer uma questão de gráfico para introduzir o conceito de integral!
Nesse caso, a função se comporta com o seguinte gráfico:
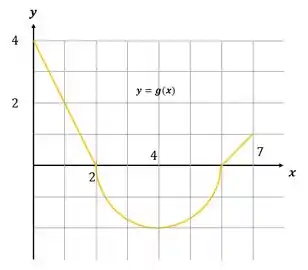
E o que é a a integral dessa função ? A integral é a área abaixo da curva!
Passo 2
Então fazendo a letra “a”, ele nos pede:
Como o intervalo de integração é a , temos que pegar esse intervalo no nosso gráfico:
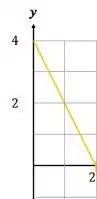
Temos então a área de um TRIÂNGULO!
O triângulo é retângulo com a base é igual a e a altura é igual a :
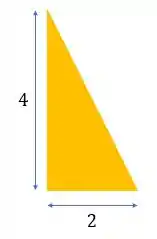
A área do trinângulo é igual ao produto da base pela altura dividido por :
Substituindo os nossos valores, vamos chamar essa primeira área como área :
Resolvendo esse cálculo:
Logo nossa primeira integral é igual a essa área:
Esse é o fim da letra “a”! Vamos para o próximo item!
Passo 3
Olhando a letra “b”, eles nos pedem a seguinte integral:
Como nosso intervalo agora é de até , temos essa área aqui:
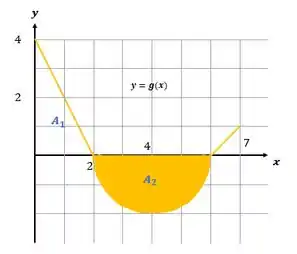
Nada mais é do que um semi-círculo de raio igual a !
Já sabemos que precisamos calcular a área desse semi-círculo para calcular a integral, mas vamos com calma.
A área do círculo é:
Logo a área do semi-círculo é a metade da área do círculo:
Então substituindo o raio igual a :
Nossa área se torna:
Mas o que falta pra gente determinar a área ? Bom, vendo que a curva está abaixo do eixo , então integral é a área negativa!
Meu consagrado, guarda essa técnica de coração, porque esse conceito é ouro!
Passo 4
Por último, vamos olhar pra letra “c”:
Olha essa dica-chave pra essa questão, na letra ele pediu pra calcular a integral no intervalo de até e na letra calcular o integral no intervalo de até . Agora nesse momento ele quer integrar de até direto, então podemos usar a propriedade de aditividade!
Ou seja:
Pela letra “a”, nós sabemos:
Enquanto a letra “b” diz que:
Juntando essas informações:
Viu como essa informação muda tudo? Leva isso dentro do coração pra prova e arrasa!
Resposta
a)
b)
c)