UFF, Niterói - Campus da Praia Vermelha, Cálculo IA, Listas de C1 - UFF (GMA) - Lista 14 - Integração por substituição e por partes, Questão 2
Mostre que as áreas das regiões dadas a seguir são iguais
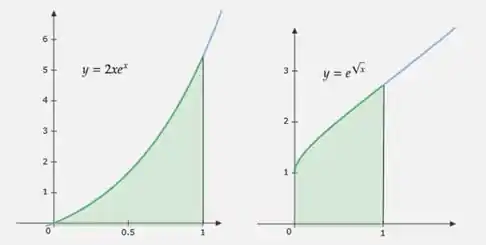
Passo 1
Beleza pessoal?! Espero que voce esteja bem e super disposto a aprender um pouco mais comigo aqui hoje. O que iremos fazer é comparar a área de duas regiões dadas por uma função, então para isso iremos realizar uma integração.
Passo 2
Para a nossa primeira área, temos que
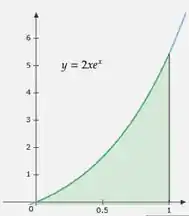
Não nos é natural resolver a integral da nossa área, pelo visto teremos que manipula-la para que tenhamos uma integral já tabelada.
A forma de resolvermos a integral, é resolve-la por integração por partes, onde ,
E ,
Agora temos que
Agora que sabemos o valor da integral indefinida, basta substituir os valores para termos a nossa área.
A = 2
Passo 3
Para a nossa segunda região, temos
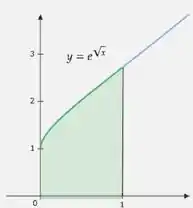
E a nossa integral para a área é dada por,
Nossa situação agora complicou um pouco mais, primeiro vamos realizar uma substituição nessa integral e ver o que acontece. Chamamos de e
Agora nossa integral tem essa cara,
Eu não sei vocês, mas acredito que eu já vi essa integral em outro lugar. Sabemos que essa integral nos dará 2 pois já resolvemos anteriormente, sendo assim temos que nossas duas áreas são realmente iguais. Obrigado por me acompanhar até aqui e até a próxima.
Resposta
Ver o desenvolvimento.