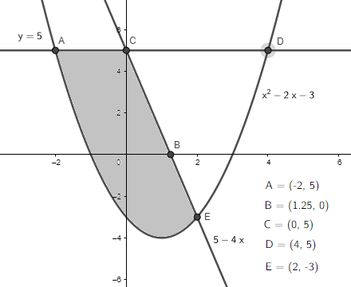
Q01) Seja a região plana dada por:
- Esboce abaixo a região . Indique explicitamente em seu desenho as coordenadas de três pontos que pertençam à fronteira da região.
- Escreva a área da região através de uma soma de duas integrais na variável . Atenção: Neste item não é necessário calcular as integrais.
- Escreva a área da região através de uma soma de duas integrais na variável . Atenção: Neste item não é necessário calcular as integrais.
- Calcule a área da região utilizando o método que preferir.
Passo 1
Opa, vamos lá. Cara, te falar, essa região ta meio feia de entender assim. Vamos fazer o seguinte: isolar tudo que tem a ver com o . Logo, as inequações:
Vão virar:
Opa, surgiram três funções diferentes, respectivamente uma parábola, uma constante e uma reta. Vamos ver as interseções entre eles? Isso vai ser importante pro esboço. Começando com a parábola e a constante:
Pela fórmula de Bháskara, as raízes desse polinômio serão:
Logo:
Então os pontos de interseção parábola e constante vão ser:
Agora vamos ver a parábola com a reta:
Pela fórmula de Bháskara, as raízes desse polinômio serão:
Logo:
Usando esses pontos na reta pra achar o valor de mais facilmente:
Logo os pontos de interseção são:
E pra fechar, vamos ver os pontos de interseção reta-constante:
O único ponto de interseção vai ser então:
Bem, então todos os nossos pontos vão ser:
Desse bolo de pontos, eu vou retirar o porque o dele é muito alto. Como a constante ajuda a delimitar a região, um valor de tão alto não vai ajudar a gente a visualizar a região . No lugar dele, vamos adicionar a interseção da reta com o eixo :
Fechamos então com os seguintes pontos guias:
E esboçando os gráficos pra marcar esses pontos vamos ter:
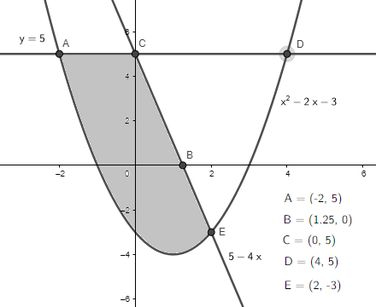
Passo 2
Agora a gente vai ter que deixar indicada a área como uma soma de duas integrais na variável . Como são só duas, minha dica pra vocês é usar o eixo de guia. Sendo assim, vamos dividir o intervalo de em que a região está contida em duas:
Logo a área vai ficar:
Vai faltar só a gente identificar quem é e quem é . Vamos começar com . Se eu fosse fazer a seguinte integral:
Estaria representando a seguinte área:
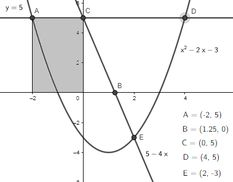
Mas ai estaria faltando adicionar essa área:
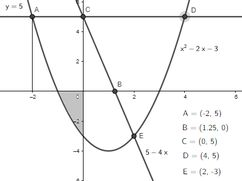
E remover a área:
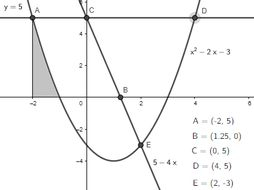
Só que veja bem, dá pra ver que a parábola toca o eixo em algum ponto entre e . Nem precisamos descobrir esse ponto pra entender aqui, então vamos chamar de . Sendo assim, pra remover essa área, basta a gente retirar a integral de até da parábola:
E pra adicionar aquela areazinha abaixo do eixo , se só fizermos a integral:
O resultado vai dar negativo! Afinal a região em questão está abaixo do eixo ! Pra compensar a gente tem que somar aquela areazinha com um sinal de negativo. Fechamos então:
Agora vamos cuidar do intervalo . Pra isso, como a reta ta partindo do eixo e descendo até tocar o eixo em , como vimos, se fizermos só a integral:
Vamos estar falando da seguinte área:
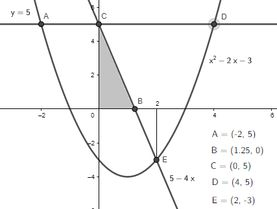
Só que a essa área precisamos adicionar essa:
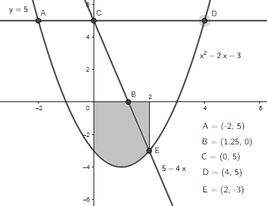
E remover essa:
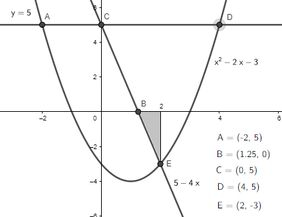
A área a ser adicionada é negativa se só fizermos a integral da parábola de até . Então pra compensar, a gente adiciona com um sinal de negativo:
A área que temos que retirar é negativa também se só fizermos a integral da reta de até . Pra compensar, a gente coloca um sinal de negativo como fizemos antes. Mas como dessa vez queremos retirar, vamos subtrair uma integral negativa! Sendo assim, vamos ter:
E logo fechamos a área em função de , vai dar:
Passo 3
Puts agora a questão enrolou a gente. Pra podermos refazer a área em função de , temos que ser capazes de pegar todas as funções inversas. Pra constante nem preciso me preocupar com nada:
Pra reta é mole:
Pra parábola que complica um pouco porque precisamos isolar esse de alguma forma. Bem, vamos pensar assim: e se fizéssemos aparecer um trinômio quadrado perfeito nessa parábola. Saca só:
Ok mas isso não é a nossa parábola né? Mas pode ser, basta subtrair 4 dos dois lados:
Agora da pra manipular:
Logo geramos duas funções de diferentes:
No final das contas ao invertermos tudo ficamos com:
Bora fazer um mini esboço pra entender direito o que fizemos. Quando a gente inverte uma função é como se tivéssemos pegando ela e girando no sentido anti-horário e depois espelhando com o eixo vertical. Os pontos que marcamos? Só mudar as coordenadas deles, levando em consideração que agora escreveremos eles como :
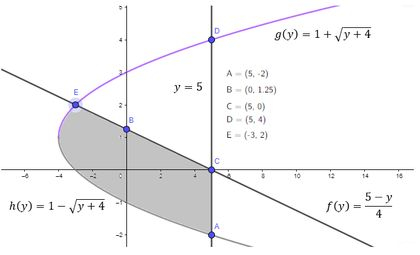
Note que tanto quanto não estão definidos para porque se não a raiz par daria negativo, o que não rola! Perceba ainda que:
Sendo assim, o ponto , que não ta marcado na figura, vai ser o ponto mais a esquerda possível da função, o que implica que vai entrar nos nossos limites de integração. Se o ponto é o mais extremo direito e tem coordenadas toda a minha região está delimitada no intervalo:
Note que o ponto tem coordenadas . Pela simetria entre e , é seguro afirmar que toca o eixo (agora o horizontal) em . Show, então vou dividir meu intervalo da região em dois:
E a área vai ficar:
Pra primeira integral, veja bem o que temos nesse intervalo:
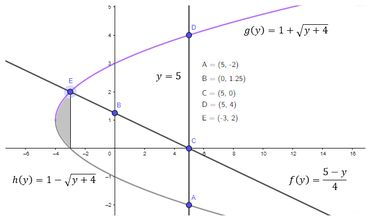
E o que é esse pedacinho se não esse:
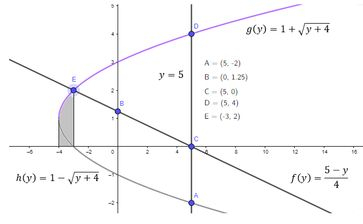
Representado pela integral:
Menos esse pedacinho:
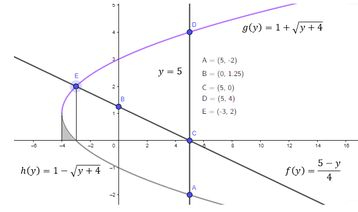
Representado pela integral:
Sendo assim vamos ter:
Agora pra outra integral, é até mais tranquilo, porque podemos entender:
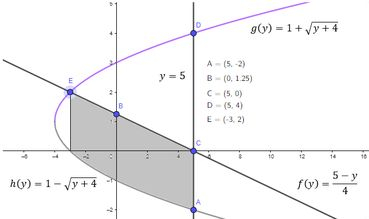
Como a soma da área:
Representado pela integral:
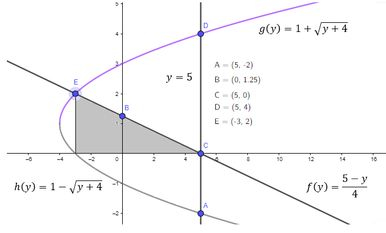
E a área:
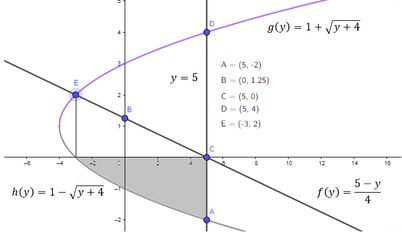
Representado pela integral:
Lembrando que o sinal de negativo ta aí pra compensar o resultado negativo da integral pura. Sendo assim, vamos ter:
Fechamos a área então, ela vai ser:
Passo 4
Pra partir pro abraço e fechar essa questão, basta a gente escolher qual das expressões de área queremos usar. Como a da letra não envolve raízes, ela vai ser a mais tranquila pra gente:
Podemos reescrever essa área para:
Usando a regra de integração para polinômios, vamos ter:
Como o resultado da integral é tudo em função de , a parcela com limite de integração igual a some, sobrando: