Q02) Considere com
a) Determine o domínio, a imagem e a expressão da função (a função inversa de )
b) Esboce abaixo os gráficos das funções e
c) Considere a região plana definida abaixo:
c.1) Seja a abscissa do único ponto de interseção entre os gráficos das funções e . Escreva a área de como uma soma de integrais na variável
c.2) Calcule a área da região em termos de
Passo 1
Bora lá. Pra começar, como estamos falando de função inversa, temos que trocar o domínio e a imagem de lugar. Mas não sabemos a imagem ainda! Oras, sabendo o domínio a gente chega lá. Seja o domínio:
Fazendo:
Vemos que:
E logo:
Quanto a expressão de , é mole, basta a gente usar a função inversa trigonométrica correspondente. Logo:
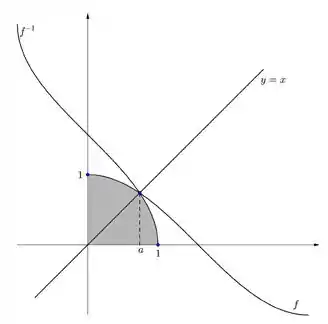
Show, agora vamos focar no esboço do gráfico das funções. Como uma função inversa é a imagem espelhada em relação a reta e sabemos esboçar por ser uma função trigonométrica oscilatória, o esboço fica:
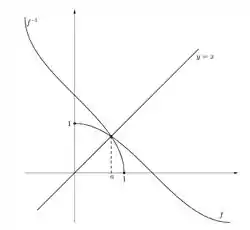
Note que o ponto , comum as duas curvas, tem que acontecer uma vez que é nesse ponto que toca no eixo de simetria. É como se fosse um espelho, seu reflexo também tocará no espelho se você tiver tocando, tendeu? Ah e como pra poupar papel não precisamos desenhar taaaanto assim, principalmente para
Passo 2
Pra gente entender a região , vamos pensar assim: como ela é definida por
Então ela é, no máximo, a região dentro dessa caixinha aqui:
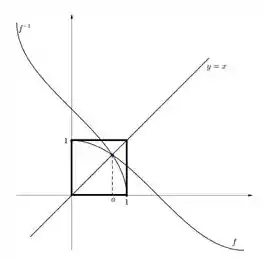
Mas como ta valendo
De até , onde a curva está por cima, basta a gente rachurar a região abaixo de :
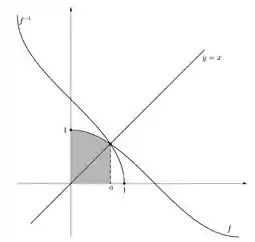
E essa área rachurada vai ser então representada pela integral:
Agora, de até , a curva está por baixo! Então basta a basta a gente rachurar a região abaixo de , completando a região toda:
E o pedaço que acabamos de rachurar tem área representada pela integral:
A área total é dada então por:
Passo 3
Agora basta calcular essa área e partir pro abraço:
Calcular a primeira integral é bem direto não é mesmo? Vamos ter:
Agora, a segunda integral, complica um tico a mais. Mas pensa aqui comigo, sabemos a derivada de ? Sabemos!
Então que tal a gente usar um método de integração que envolva derivar o ? Bora tentar integrar por partes. Seja:
E seja a regra da integração por partes:
Temos:
A integral que sobrou é mais tranquila de resolver porque não tem funções trigonométricas. Dá pra tirar de letra com uma substituição simples, quer ver? Se:
E logo:
Voltando pra variável original:
E logo a integral fica:
Aplicando os limites de integração:
Por fim:
E a área total vai ser:
Resposta