Questão 3) Calcular a área da região limitada do plano, delimitada pelos gráficos das seguintes funções: , e .
Passo 1
Bem, antes de passarmos para o problema da área em si, vamos desenhar essa região para ver com quem a gente está lidando, ok?
As duas primeiras curvas, e são tranquilas, são duas retas:
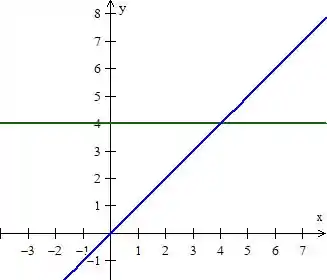
Já é que se tem que ter mais cuidado, poies ela representa o gráfico de só que um pouco mais côncava:
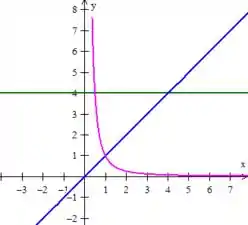
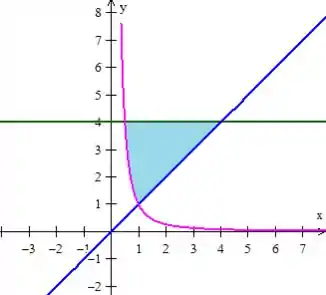
Passo 2
Bem, mas você já deve ter reparado na representação da região que surgiu alguns pontos de encontro... Antes de prosseguirmos para calcular área, devemos determinar que pontos são esses, afinal eles serão importantes, saca?
- O ponto de encontro da reta verde com a curva rosa...
- O ponto de encontro da azul com a rosa...
- Por fim, o ponto de curva verde com a reta azul...
Passo 3
Para a determinação da área de , saiba que uma área aqui sempre será dada por...
Onde é a função que está por cima e , a função que está por baixo. Mas se você reparar no esboço da região novamente... Vai notar que a função que está por baixo, muda quando chegamos no ...
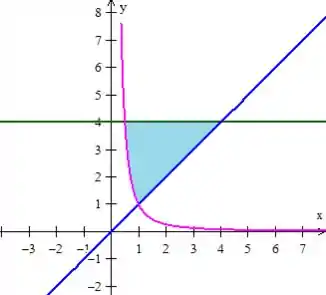
Por isso vamos ter que separar essa integral em duas, a primeira vai de a e a segunda de a ...
Onde a função de cima é e curva de baixo até é a e depois de até é , saca?
Passo 4
Agora é só calcular!
Calculando a primeira integral...
Calculando a outra integral...