P3 – Cálculo 1 – Unicamp – 2022.2 – Questão 4
Questão 4
Seja a região limitada pela curva e pelas retas , e .
a) Faça um esboço da região
b) Determine a área de
c) Calcule o volume obtido pela rotação da região em torno do eixo .
Passo 1
Bom galerinha da Unicamp, nessa questão vamos utilizar a integral para calcular a área e o volume de revolução de uma região... mas calma, que isso nem é tão complicado assim.
Na letra a), temos que fazer um esboço da região. Ela é delimitada por 4 curvas.
A primeira curva é , que nada mais é que a parábola só que transladada em uma unidade para cima.
A segunda curva é , que é uma reta que faz 45º e passa pela origem.
A terceira curva é que é uma reta vertical que passa por e a quarta curva é que também é uma reta vertical.
Portanto, teremos algo mais ou menos assim:
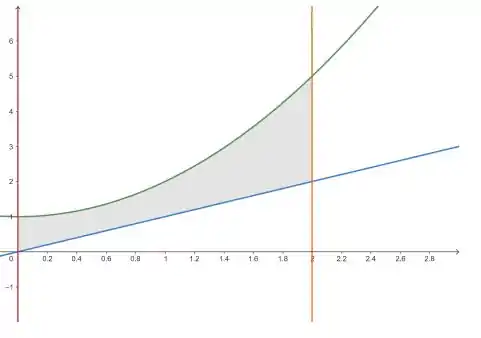
Onde em verde temos a parábola , em azul temos a reta e em vermelho e laranja temos e .
Passo 2
Para calcular a área dessa região, podemos perceber que ela nada mais é que a área abaixo da parábola menos a área abaixo da reta e tudo isso ocorre indo de até , portanto:
Se você quiser, pode juntar tudo numa integral só, não faz diferença.
Essa integral é a integral de polinômio que a gente já sabe resolver, vai resultar em:
E por fim substituindo os limites de integração, teremos:
Passo 3
Para calcular o sólido de revolução ao redor do eixo , podemos perceber que o sólido obtido pela revolução dessa região em torno do eixo vai ser composto de diversos anéis, onde cada anel possui o centro no eixo e raio externo e raio interno , de modo que a área de um desses anéis é dada por:
Portanto, o volume desse sólido será a integração da área dos anéis indo de até .
E substituindo os limites de integração, teremos:
Resposta
b)
c)