Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 223123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 3:

Sejam f e g funções dadas por

f x = 1 + 2 1 - x

e

g x = 1 + 2 x - 1

e considere R a região dada por

R = x ,   y ∈ R   |   f x ≤ y ≤ g x ,   x ≤ 3     e       y ≤ 3 .

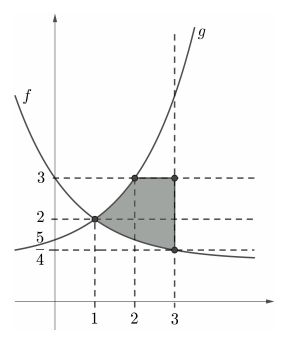
  1. Esboce a região R .
  2. Escreva a área da região R como uma soma de duas integrais na variável x .
  3. Escreva a área da região R como uma soma de duas integrais na variável y .
  4. Calcule a área da região R .

Passo 1

a )

Antes de começarmos a desenhar a região R como um todo, vamos primeiro desenhar essas duas curvas ali de cima...

f x = 1 + 2 1 - x

e

g x = 1 + 2 x - 1

Passo 2

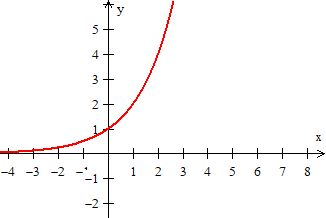
Vamos começar com a primeira curva, a de f . A função 2 x é uma exponencial e seu gráfico é semelhante ao gráfico de e x ...

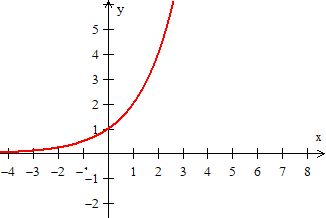
2 - x é a reflexão do gráfico de cima ao redor do eixo y ...

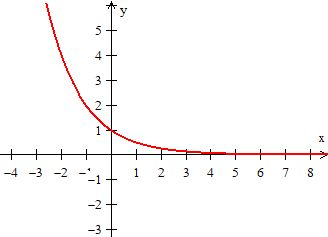
2 1 - x é um deslocamento de uma unidade do gráfico como um todo para a direita...

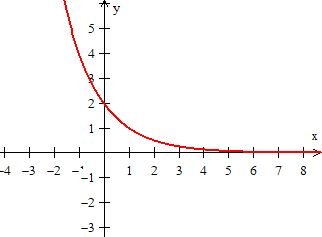
Somando 1 na função, é como se jogássemos o gráfico todo uma unidade acima...

Eis o gráfico de f x ;)

Passo 3

Fazendo a mesma coisa, determinamos o gráfico da g x ...

O gráfico de 2 x ...

2 x - 1 é um deslocamento da curva de uma unidade para a direita...

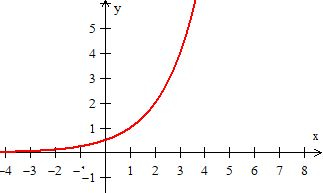
g x = 1 + 2 x - 1 será...

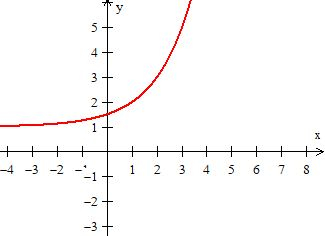
Passo 4

Agora, com essas curvas prontas, podemos desenhar a região R ...

R = x ,   y ∈ R   |   f x ≤ y ≤ g x ,   x ≤ 3     e       y ≤ 3 .

Como y está acima de f e abaixo de g , só podemos estar falando de...

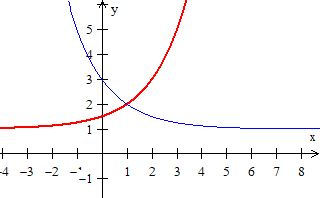
Bem, mas as outras duas restrições foi que a região R está até x = 3 e está baixo da reta y = 3 ...

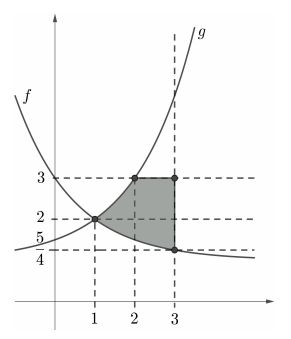
Eis a Região R , sacou? :D

Passo 5

Bem, mas você já deve ter reparado na representação da região R que surgiu alguns pontos de encontro... Antes de prosseguirmos para calcular área, devemos determinar que pontos são esses, afinal eles serão importantes, saca?

Bem, o ponto de encontro das duas exponenciais, pode ser encontrado se fizermos um sisteminha com suas equações...

f x = 1 + 2 1 - x   g x = 1 + 2 x - 1

Igualando uma função com a outra...

1 + 2 1 - x = 1 + 2 x - 1 →

2 1 - x = 2 x - 1

Desprezando a base que é a mesma...

1 - x = x - 1       →             2 x = 2         →

x = 1

A coordenada y desse ponto é...

y = f x = 1 + 2 1 - x = 1 + 2 0 = 2

Passo 6

O ponto de encontro da g x com a reta y = 3 ...

y = g x = 1 + 2 x - 1     →

3 = 1 + 2 x - 1       →           2 = 2 x - 1

Então...

x - 1 = 1     →       x = 2

Quanto ao ponto de encontro de f com a reta x = 3 ...

f x = 1 + 2 1 - x         →           f 3 = 1 + 2 1 - 3   →

1 + 2 - 2 =

1 + 1 4 =

5 4

Prontinho! :) Podemos prosseguir viagem para determinar as integrais pedidas !

Passo 7

b )

Para a determinação dessa soma de integrais que calcula a área de R , saiba que uma área aqui sempre será dada por...

A R = ∫ a b h 1 x - h 2 x   d x

Onde h 1 é a função que está por cima e h 2 , a função que está por baixo. Mas se você reparar no esboço da região R novamente... Vai notar que a função que está por cima, muda quando chegamos no x = 2 ...

Por isso vamos ter que separar essa integral em duas, a primeira vai de 1 a 2 e a segunda de 2 a 3 ...

A R = ∫ 1 2 g x - f x   d x + ∫ 2 3 3 - f x   d x   →

A R = ∫ 1 2 1 + 2 x - 1 - 1 - 2 1 - x   d x + ∫ 2 3 3 - 1 - 2 1 - x   d x   →

A R = ∫ 1 2 2 x - 1 - 2 1 - x   d x + ∫ 2 3 2 - 2 1 - x   d x

Passo 8

c )

Vamos ter descrever agora a integral considerando a variável y , ou seja...

A R = ∫ a b h 1 y - h 2 y   d y

Para você vê quem é a h 1 y e h 2 y , é como se tivéssemos invertendo o gráfico...

Perceba que a h 1 y , continua sendo a função que está por cima, mas dessa vez sob essa perspectiva. Assim sendo, e considerando g - y     e     f - y as funções inversas de g x e f x , perceba que também podemos separar a integral em duas partes...

A R = ∫ 5 4 2 3 - f - y   d y + ∫ 2 3 3 - g - y   d y  

Sacou?

Vamos apenas determinar essa f - y e g - y !

Passo 9

Bem...

f x = 1 + 2 1 - x

Vamos trocar esse f x = y para facilitar a notação...

y = 1 + 2 1 - x     →

2 1 - x = y - 1

Aplicando a o log 2 ⁡   em ambos os lados já que o logaritmo é o inverso da potenciação...

log 2 ⁡ 2 1 - x = log 2 �� y - 1

Por propriedade Logarítmica...

1 - x log 2 ⁡ 2 = log 2 ⁡ y - 1   →

1 - x = log 2 ⁡ y - 1       →

x = 1 - log 2 ⁡ y - 1

Então, essa é a expressão que define a função inversa, como ela veio da f x , podemos chamar o x de...

f - y = 1 - log 2 ⁡ y - 1

Passo 10

Podemos fazer o mesmo para a g x ...

g x = y = 1 + 2 x - 1   →

2 x - 1 = y - 1

Aplicando o log...

log 2 ⁡ 2 x - 1 = log 2 ⁡ y - 1   →

x - 1 = log 2 ⁡ y - 1   →

x = log 2 ⁡ y - 1 + 1

g - y = x = log 2 ⁡ y - 1 + 1

Sacou?

Passo 11

Então a área em termos de y se calcula...

A R = ∫ 5 4 2 3 - f - y   d y + ∫ 2 3 3 - g - y   d y  

A R = ∫ 5 4 2 3 - 1 + log 2 ⁡ y - 1   d y + ∫ 2 3 3 - log 2 ⁡ y - 1 - 1   d y

A R = ∫ 5 4 2 2 + log 2 ⁡ y - 1   d y + ∫ 2 3 2 - log 2 ⁡ y - 1   d y

Passo 12

d )

Depois de determinar duas expressões integrais que calculam a área, vamos colocar as mãos na massa e encontrar o resultado dela. Vamos usar a primeira fórmula que está mais simples...

A R = ∫ 1 2 2 x - 1 - 2 1 - x   d x + ∫ 2 3 2 - 2 1 - x   d x

Bem... Arrumando essa integral aí...

A R = ∫ 1 2 2 x - 1   d x + ∫ 1 2 - 2 1 - x   d x + ∫ 2 3 - 2 1 - x   d x + ∫ 2 3 2   d x

Essas duas integrais do meio aí podem se juntar...

A R = ∫ 1 2 2 x - 1   d x + ∫ 1 3 - 2 1 - x   d x + ∫ 2 3 2   d x

A última integral se resolve fácil...

A R = ∫ 1 2 2 x - 1   d x + �� 1 3 - 2 1 - x   d x + 2 3 - 2

A R = ∫ 1 2 2 x - 1   d x + ∫ 1 3 - 2 1 - x   d x + 2

Para calcular essa primeira integral aí, vamos usar um artefato algébrico que é transformar uma potência qualquer em base e ...

e ln ⁡ 2 x - 1 = 2 x - 1   →

e x - 1 ln ⁡ 2 = 2 x - 1

Substituindo...

A R = ∫ 1 2 e x - 1 ln ⁡ 2   d x + ∫ 1 3 - 2 1 - x   d x + 2

Fazendo uma substituição de...

x - 1 ln ⁡ 2 = a           →             d a = ln ⁡ 2 d x               o u           d x = d a ln ⁡ 2

Trocando também os limites de integração...

x = 1             a = 1 - 1 ln ⁡ 2 = 0

x = 2             a = ln ⁡ 2

A R = ∫ 0 ln ⁡ 2 e a   d a ln ⁡ 2 + ∫ 1 3 - 2 1 - x   d x + 2

A R = e a ln ⁡ 2 0 ln ⁡ 2 + ∫ 1 3 - 2 1 - x   d x + 2 =

A R = e ln ⁡ 2 ln ⁡ 2 - 1 ln ⁡ 2 + ∫ 1 3 - 2 1 - x   d x + 2 =

A R = 2 ln ⁡ 2 - 1 ln ⁡ 2 + ∫ 1 3 - 2 1 - x   d x + 2 =

A R = 1 ln ⁡ 2 - ∫ 1 3 2 1 - x   d x + 2 =

Calculando de forma semelhante a outra integral...

e ln ⁡ 2 1 - x = 2 1 - x

e 1 - x ln ⁡ 2 = 2 1 - x

A R = 1 ln ⁡ 2 - ∫ 1 3 e 1 - x ln ⁡ 2   d x + 2 =

1 - x ln ⁡ 2 = b         →             d b = - ln ⁡ 2 d x           o u           d x = - d b ln ⁡ 2

Limites...

x = 1           →                   b = 1 - 1 ln ⁡ 2 = 0

x = 1           →                   b = - 2 ln ⁡ 2

A R = 1 ln ⁡ 2 - ∫ 0 - 2 ln ⁡ 2 e b   - d b ln ⁡ 2 + 2 =

A R = 1 ln ⁡ 2 + e b ln ⁡ 2 0 - 2 ln ⁡ 2 + 2 =

A R = 1 ln ⁡ 2 + e - 2 ln ⁡ 2 ln ⁡ 2 - 1 ln ⁡ 2 + 2 =

A R = 1 4 ln ⁡ 2 + 2

Resposta

a )

b )

A R = ∫ 1 2 2 x - 1 - 2 1 - x   d x + ∫ 2 3 2 - 2 1 - x   d x

c )

A R = ∫ 5 4 2 2 + log 2 ⁡ y - 1   d y + ∫ 2 3 2 - log 2 ⁡ y - 1   d y

d )

1 4 ln ⁡ 2 + 2

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x