UFRJ, Sem Campus, Cálculo 1, Listas de C1 - IM/UFRJ - Lista 5 - P3, Questão 10
As regiões A, B e C da figura são limitadas pelo gráfico de f e pelo eixo x. Se a área de cada
região vale . (unidades de área), qual é o valor de ?
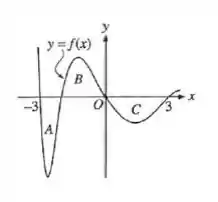
Passo 1
Como as áreas das regiões A, B e C valem 2 unidades de área cada, podemos utilizar essa informação para determinar a integral de
A região A tem uma área de 2 unidades de área e está abaixo do eixo x, o que significa que a integral de x em relação a sobre o intervalo é igual a -2:
Passo 2
A região B também tem uma área de 2 unidades de área, mas está acima do eixo x, portanto a integral de em relação a sobre o intervalo é igual a 2:
A região C, que é a região entre a curva e o eixo x, tem uma área de 2 unidades de área, o que significa que a integral de em relação a sobre o intervalo é igual a 0:
Passo 3
Agora, precisamos calcular a integral de
Podemos fazer isso somando 1 à função e, em seguida, integrando:
Usando as informações das integrais de que calculamos acima:
A integral de uma constante é a própria constante vezes o intervalo de integração:
Portanto, a integral de é igual a 4.
Resposta
Portanto, a integral de é igual a 4.