UFSC – Cálculo 1 – Lista 4.3 – Questão 5a – Parte 1
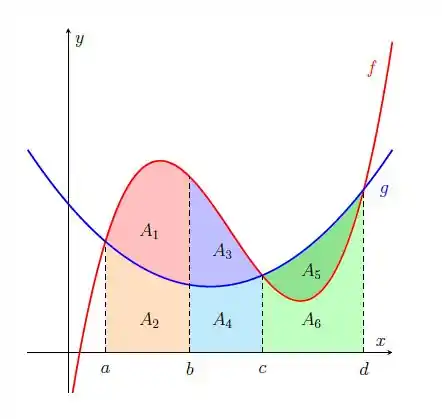
- Escreva o resultado das integrais em termos das medidas das áreas
Passo 1
E aí pessoal, tudo bem?
Essa questão é de análise de gráfico! Pode ser confuso, mas vou fazer passo a passo com você!
A ideia é olhar o gráfico dado e verificar quais áreas fazem parte daquele intervalo proposto, observando sempre qual função ele está se referindo.
Agora vamos analisar as áreas embaixo da função que está em VERMELHO
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar escrevendo o resultado dessa integral aqui
Os intervalos são de até :
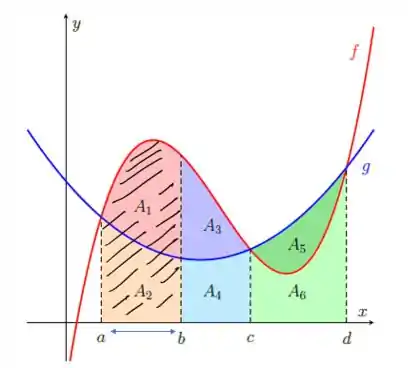
A área abaixo da curva é exatamente a SOMA das áreas e , então podemos escrever essa integral assim:
Notem que queremos a área sob a curva ! Então por enquanto, vamos ignorar a existência da !
Tranquilo?
Passo 3
Agora vamos escrever essa integral aqui
Agora vamos olhar os intervalos de até :
A área abaixo da curva é a SOMA das áreas e, então podemos escrever essa integral assim:
Beleza? Vamos para a última integral?
Passo 4
Agora o último intervalo a ser considerado:
É de até , sempre olhando abaixo da curva :
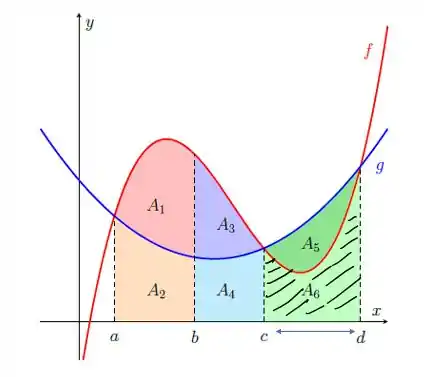
note que abaixo da curva VERMELHA, nesse intervalo, temos apenas uma área:!
Então a integral de nesse intervalo será apenas essa área:
E é isso! Terminamos a questão!
Espero ter ajudado! Vamos para a próxima?