UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 1.3b
Represente a área da região por uma integral:
é a região de intersecção dos círculos e
Passo 1
E aí galerinha, tudo certo com vocês?
Nessa questão recebemos a descrição de uma região . É falado que é a região de intersecção dos seguintes círculos:
A partir dessas informações devemos representar a área de por meio de integrais.
Para fazer isso, podemos usar o recurso da integral. Se uma região é definida de tal forma que:
Podemos escrever que a área dessa região é dada por:
onde e são determinados pela intersecção de e .
Massa!
Vamo nessa!
Passo 2
Bom, vamos começar plotando em um mesmo gráfico os dois círculos dados no enunciado. Lembrando que a equação geral de um círculo é dada por:
onde é o centro do círculo e o raio dele.
Assim, temos:
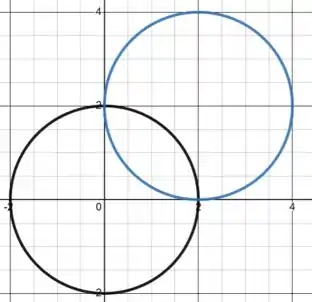
Portanto, a região que está na intersecção dos círculos vai de até .
Muito bem!
Passo 3
Como essa região está no primeiro quadrante, podemos reescrever as equações do círculo.
Para o círculo centrado em , o círculo preto, temos:
Já para o círculo centrado em , o círculo azul, temos:
Como é a parte inferior da circunferência no intervalo de , temos:
Daí, como a curva do círculo azul está abaixo da curva do círculo preto, usando a ideia de área lá do passo , isto é:
Podemos escrever:
Daí, voltando para a integral, vem que:
Prontinho! Conseguimos representar a área da região por uma integral 😊