UFBA, Sem Campus, Cálculo B, Listas de Cálculo B - UFBA - Lista 1, Questão 1.3a
Represente a área da região por uma integral:
é a região no primeiro quadrante limitada pelo eixo , pela reta e pelo círculo .
Passo 1
Olá pessoal, como vocês estão?
Nessa questão recebemos a descrição de uma região . É falado que :
- Está no primeiro quadrante;
- é limitada pelo eixo ;
- é limitada pela reta
- é limitada pelo círculo .
A partir dessas informações devemos representar a área de por meio de integrais.
Para fazer isso, podemos usar o recurso da integral. Se uma região é definida de tal forma que:
Podemos escrever que a área dessa região é dada por:
onde e são determinados pela intersecção de e .
Massa!
Vamo nessa!
Passo 2
Bom, vamos começar fazendo um rápido esboço da região .
Plotando todas as curvas que limitam em um mesmo gráfico, temos:
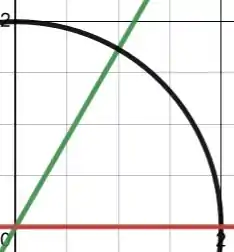
Portanto, nossa região é justamente o espaço entre essas curvas.
Vamos calcular o ponto de intersecção da reta com o círculo em questão.
Logo:
Muito bom!
Passo 3
Assim, de até , a nossa região está entre a reta e o círculo .
Como estamos no primeiro quadrante, podemos ainda escrever a equação do círculo como:
Além disso, podemos escrever a reta como uma função de :
Assim, usando que:
Como o círculo é a curva mais externa, temos:
Podemos escrever essa área da seguinte forma
Prontinhoo! Essa é a área de representada por meio de integrais 😊