A reta de equação divide a região compreendida entre as parábolas de equações e em duas partes. Mostre que as áreas das regiões obtidas são iguais e calcule o seu valor.
Passo 1
Vamos começar achando onde as parábolas se encontram para podermos fazer o gráfico disso direito.
Resolvendo essa equação vamos ter
O gráfico dessas duas parábolas vai ficar
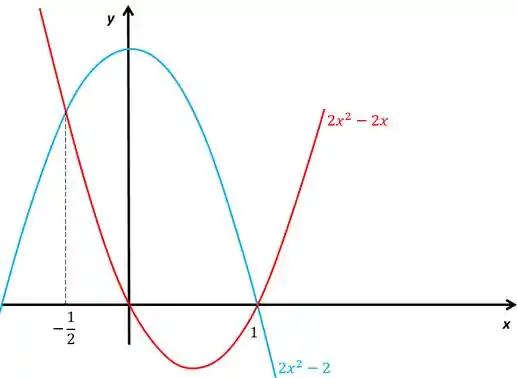
Passo 2
Vamos agora descobrir onde a reta corta cada uma das parábolas, primeiro a parábola vermelha.
Opa caiu na mesma equação de segundo grau, então a reta passa no ponto de encontro entre as parábolas, o gráfico vai ficar.
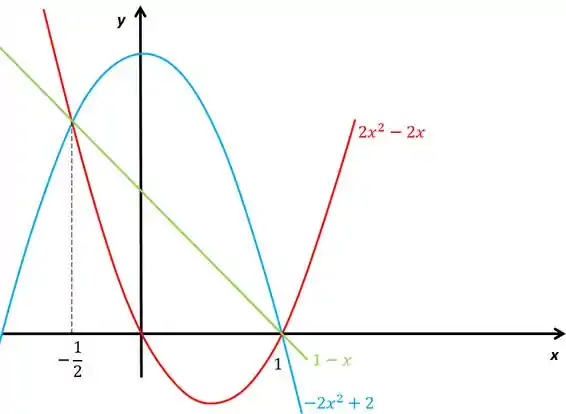
Passo 3
Vamos achar cada uma das áreas agora, primeiro a área entre a reta e a parábola azul, como vai ser a integral?
Passo 4
Agora vamos para área entre a reta e a parábola vermelha, como vai ser a integral?
Que dá a mesma integral dali de cima, então não precisamos resolver sabemos que
Isso nos diz que as áreas são iguais.
Resposta
Ei, a resposta está no passo a passo :)