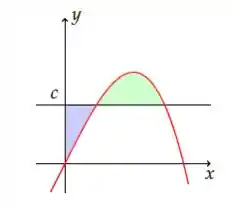
A reta horizontal intercepta a curva no primeiro quadrante como mostra a figura.
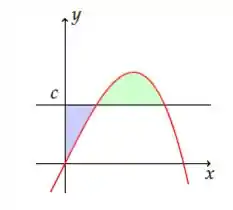
Determine para que as áreas das duas regiões sombreadas sejam iguais.
Passo 1
 Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema deu essa região
Oi, tudo bem? Essa questão parece complicada, mas vou descomplicar para você! O problema deu essa região
Com a curva vermelha e pediu para que as áreas verde e roxo sejam iguais e achar o que deixa isso certinho
Mas como resolver isso?

Precisamos pensar o seguinte, supondo
E o retângulo . Temos que a área da região em ROXO seria
Já a região VERDE seria
Beleza?

Nossa missão é igualar essas duas áreas e resolver para !
É isso! Bora lá?

Mas relaxa, vou fazer passo a passo com você!
Passo 2
Vamos começar igualando as áreas
Resolvendo as integrais temos
Aplicando os limites de integração e simplificando temos
Beleza?

Agora manipular um pouco para termos em função de ! Multiplicando os dois lados por
Tudo bem até aqui?

Passo 3
Sabemos assim temos
Agora substituindo em temos
Simplificando temos
E por fim substituindo em
Show! E é isso pessoal! Espero ter ajudado!