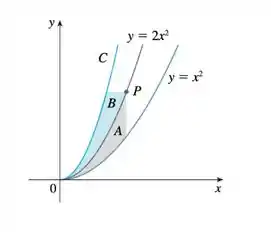
A seguinte figura mostra uma curva C com a seguinte propriedade: para cada ponto P na curva , as áreas e são iguais, ache uma equação para C.
Passo 1
Opa galera, aqui é uma questão de cálculo integral onde nós temos as informações e precisamos de uma função que se encaixe nas especificações dada no problema.
Opa galera, aqui é uma questão de cálculo integral onde temos três curvas:
A característica que une essas curvas é que a área entre e deve ser igual a área entre e . (Tem alguns detalhezinhos na formação dessas áreas que comentaremos mais a frente, beleza?)
O objetivo da questão é que encontremos quem é essa curva .
Puts... Como podemos fazer isso?
Para resolver o probleminha precisamos lembrar como se calcula uma área com o conceito de integral, você se lembra?

CAAAAAAAAAALMINHA, não precisa se preocupar vamos lembrar desse conceito bem importante aqui, para o cálculo de uma área de uma figura geométrica entre um intervalo temos que essa área corresponde a seguinte integral definida:
Então como isso resolve meu problema né?
É o seguinte ele num falou que as áreas são iguais? Então vamos calcular a área e depois calcular a área e igualar para ver no que dá.

Deeeeeeeixa disso, fica tranquilo, vamos resolver juntinhos ok?
Eu sei que essas questões de integração são meio chatinhas então vamos resolver um passinho de cada vez. Começando pelos desenhos da região de integração.
Dica: sempre desenhe, fica muuuuito melhor a visualização do problema.
Passo 2
Primeiramente vamos realizar o desenho das funções, basicamente é reescrever a imagem do problema para podermos rabiscar a vontade. Deixando dessa forma:
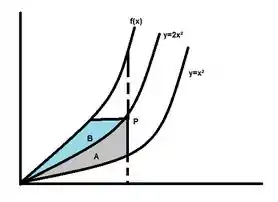
Agora vamos quantificar as Áreas utilizando a formulinha que aprendemos no cálculo integral temos que a área é dada pela seguinte expressão:
Onde a e a são as funções que limitam a região superiormente e inferiormente.
Aplicando para o mesmo raciocínio temos que:
OPAAAAAAAAAAAAAAAAAA se realizarmos isso temos um errozinho, consegue observar? Isso ai, quando eu realizo essa operação eu estou não só calculando a área da região azul mas também da região roxinha como mostrado na figura abaixo:
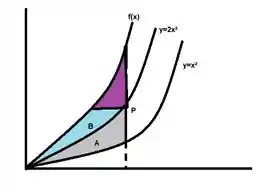
E precisamos remover esse pedacinho de Area roxchinha, para isso precisamos de algumas suposições, primeiramente é que esse triangulo roxinho esteja a uma altura edo eixo .
A segunda é que precisamos supor que a reta intercepte a função em algum ponto que não seja o infinito, até porque nós não contamos até o infinito né?
E para finalizar essas funções precisam ser todas bem comportadinhas, sendo assim temos que a área da região corresponde a:
E finalmente conseguimoooos.

Passo 3
Igualando as áreas temos que:
Utilizando a linearidade das integrais para resolver as somas, temos que:
Isolando a integral temos que:
Passo 4
Para finalizar, precisamos utilizar o teorema fundamental do cálculo que para esse caso temos que:
Sendo assim derivando com as respectivas propriedades e utilizando a regra da cadeia temos que:
É isso pessoal! Espero que vocês tenham entendido bem direitinho essa questão 😊Valeeu, até a próxima!
Resposta
A resposta é