UFPE – Cálculo 1 – 2020.2 – Terceiro Exame – Exercício 2
Seja o conjunto do plano limitado pela reta e pelo gráfico de , com . Desenha e calcule sua área.
Passo 1
Fala galerinha, beleza?
Esse tipo de problema é bem tradicional na parte de aplicações de integrais. Temos que desenhar uma região no plano cartesiano e em seguida calcular sua área.
Primeiro damos uma olhada na parábola . Suas raízes são soluções da equação
O vértice, que corresponde ao máximo, ocorre em
Daí, fica fácil esboçar a região limitada pela parábola, pelo eixo (reta ) e pelas retas verticais e :
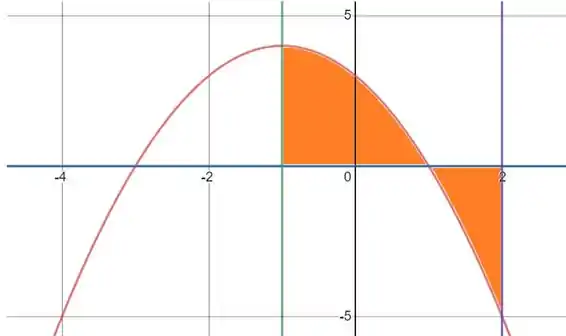
Passo 2
Para calcular a área da região laranja, temos que quebrar duas integrais: um de até , e outro de até . Na primeira integral, a função que integramos é . Já na segunda, integramos o oposto: . Logo,
Fazendo a primitiva:
Daí, é só substituir os limites:
Logo,
Portanto,