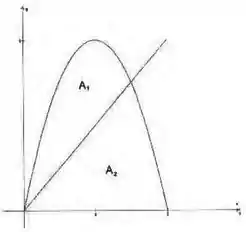
Seja e considerar a reta de equação , . Determine o valor de para o qual as áreas e mostradas na figura são iguais.
Passo 1
Vamos chamar o ponto onde a reta encontra a parábola pela segunda vez de por enquanto. Ora, a área pode ser calculada como o espaço entre parábola e reta de até . Já a área deve ser dividida em dois pedaços um que vai do eixo até a reta, no intervalo de até , e outro que vai do eixo até a parábola, com entre e , que é a segunda raiz da parábola. Vamos armar as duas equações de área:
Passo 2
Vamos agora calcular cara uma das áreas é igualá-las:
Passo 3
Nesse momento eu poderia simplesmente igualar as áreas, mas nisso nós caímos numa equação maior e mais difícil de resolver. Mas repara numa coisa, pode ser calculado como a área entre o eixo e a parábola.
Se queremos que seja igual a temos que fazer com que metade desse valor encontrado seja igual a um dos termos, o que facilita na igualdade. Vou dizer, então, que metade de é igual à área calculada em :
Agora, o detalhe é relacionar com . Bom, não é o ponto de encontro entre a reta e a parábola do problema? Vamos calcular esse em função de :
Assim, . Voltamos à igualdade: