Seja Considere a região plana
b) Esboce abaixo a região . Indique em seu desenho as coordenadas dos pontos de interseção
do gráfico de com os eixos e .
c) Escreva a área de como uma integral na variável .
d) Escreva a área de como uma integral na variável .
e) Calcule a área de .
Passo 1
b) Para encontrarmos a intersecção de com o eixo , vamos calcular , e para encontrarmos a intersecção de com o eixo , vamos calcular .
Com o eixo :
Então o ponto de intersecção com o eixo é .
Com o eixo :
Então o ponto de intersecção com o eixo é .
Passo 2
O gráfico de é assim:
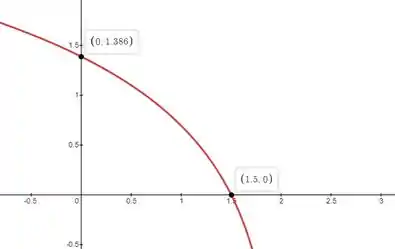
Como a região é tal que
Então ela vai ser essa partezinha verde:
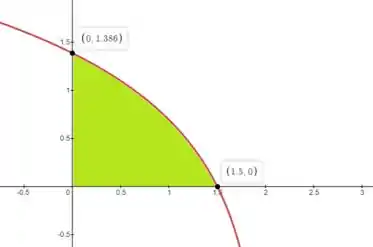
Passo 3
c) No eixo , observando no gráfico do passo anterior, a região de tem área de até , sendo dada pela integral de :
Passo 4
d) A primeira coisa que vamos fazer aqui vai ser escrever nossa função com a variável , ou seja, inverter a função:
No eixo , olhando nosso gráfico de lado, a área de vai de até não é? Então:
Passo 5
e) Vamos calcular a área de usando a integral do item d:
Resposta
b)
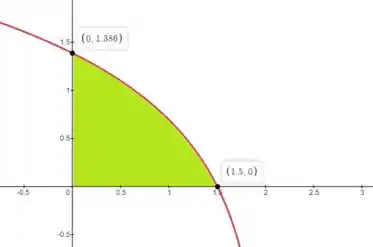
c)
d)
e)