Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 259123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Área entre curvas

Seja f diferenciável. Calcule

∫ 0 1 x f ' x d x

Sabendo que f 1 = 2 e que

∫ 0 1 f x d x

É igual a área da região R entre o gráfico de y = - x 2 e as retas y = 1 , x = 0 e x = 1

( S u g e s t ã o : d d x x f x = f x + x f ' x

Passo 1

Vamos fazer a sugestão dele, afinal está ali para ajudar né

d d x x f x = f x + x f ' x

Vamos isolar o valor que está na integral que queremos

x f ' x = d d x x f x - f x

Integrando isso, de 0 à 1

∫ 0 1 x f ' x d x = ∫ 0 1 d d x x f x d x - ∫ 0 1 f x d x

Lembra que o Teorema fundamental do cálculo nos diz que aquela integral da derivada vai ser

∫ 0 1 d d x x f x d x = 1 . f 1 - 0 . f 0 = f 1

Vamos ter

∫ 0 1 x f ' x d x = f 1 - ∫ 0 1 f x d x

Já temos f 1 , falta achar aquela outra integral.

Passo 2

Ele disse que a integral

∫ 0 1 f x d x

É igual a área entre o gráfico de y = - x 2 e as retas y = 1 , x = 0 e x = 1

Os valores de x já estão limitado, vamos ver como fica o gráfico dessa parada

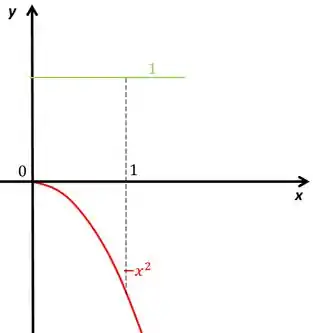
Passo 3

Vamos ter a área sendo

A = ∫ a b f c i m a - f b a i x o = ∫ 0 1 1 - - x 2 d x = ∫ 0 1 1 + x 2 d x

A = x + x 3 3 x = 0 1 = 1 + 1 3 - 0 + 0 3 = 4 3

Passo 4

Vamos ter

∫ 0 1 x f ' x d x = f 1 - ∫ 0 1 f x d x

∫ 0 1 x f ' x d x = 2 - 4 3 = 6 - 4 3 = 2 3

Resposta

2 3

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x