UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P1 2022.1, Questão 2
Seja a região de interseção das curvas e . Esboce a região e calcule sua área.
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu duas curvas polares e pediu pra gente esboçar e calcular a área da região entre elas.
Então vamos tentar identificar o tipo de gráfico representado pela equação em coordenadas polares e estimar a área entre eles calculando a integral das funções dadas:
Vamos lá!
Passo 2
Galera, no primeiro caso temos a equação , que é uma equação do tipo:
Que descreve uma circunferência de centro no eixo e que tangencia o eixo polar. Se , o gráfico está acima do polo, e se , o gráfico está abaixo do polo. Como aqui , nosso gráfico está acima do polo.
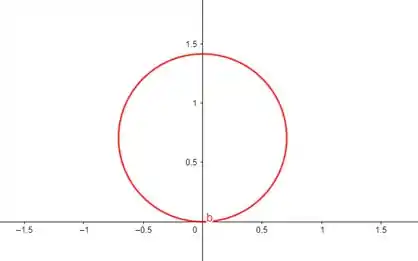
Passo 3
Nossa segunda equação é , uma equação do tipo:
onde . Esse tipo de equação descreve uma lemniscata , que é desenhada dessa forma:
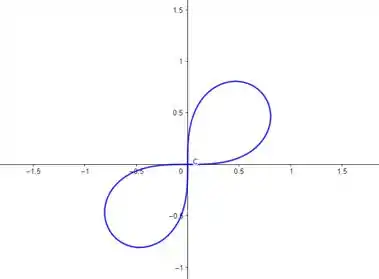
Juntando as duas curvas no gráfico, temos:
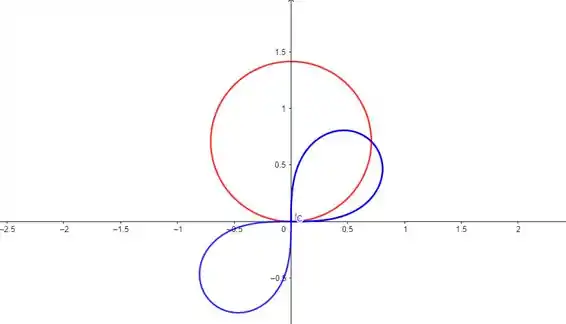
Passo 4
Agora para calcular a área entre essas duas curvas, vamos ter que primeiro encontrar seus pontos de interseção igualando as equações e :
Usando a identidade trigonométrica: , temos:
Colocando em evidência:
Então, temos ou . Pra que a primeira condição seja verdade, teremos ou . Agora para:
Dessa forma, , onde é um número inteiro. Mas repare que no gráfico, a região entre as curvas está apenas no primeiro quadrante, então vamos ter nossa área dada por:
Reescrevendo usando identidades trigonométricas, temos:
Resolvendo as integrais:
Prontinho, galera! Até a próxima! 😉