UNICAMP – Cálculo 1 – Professor Ricardo Martins – Lista de Integrais
10.4 Seja a região limitada por e por , com .
b) Seja o sólido gerado pela rotação de em torno do eixo . Calcule o volume de .
Passo 1
Falaaa... tudo bem??
Nessa questão vamos calcular o volume do sólido de revolução gerado pela rotação da região , delimitada pelas curvas e e com entre 0 e 1.
Pra isso vamos usar a fórmula para a rotação no eixo :
Onde e a diferença entre as duas curvas.
Passo 2
Fazendo um esboço dessas curvas, temos:
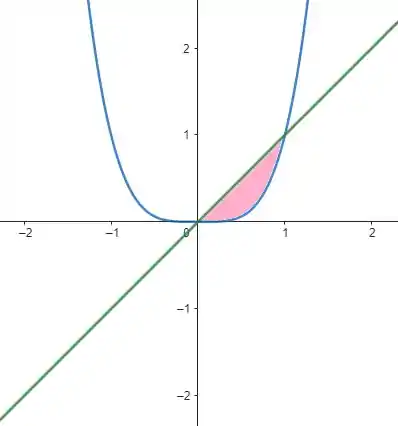
Temos a curva em verde e a curva em azul. A área que queremos calcular está em rosa.
Então o será:
Passo 3
Calculando o volume:
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x