10.4 Seja a região limitada por e por , com .
a) Calcule a área de .
Passo 1
Falaaa... tudo bem???
Nessa questão temos uma região delimitada por duas curvas, e entre e . Vamos calcular a área dessa região R.
Pra calcular essa a área dessa região usamos integral.
Passo 2
Fazendo um esboço dessas curvas, temos:
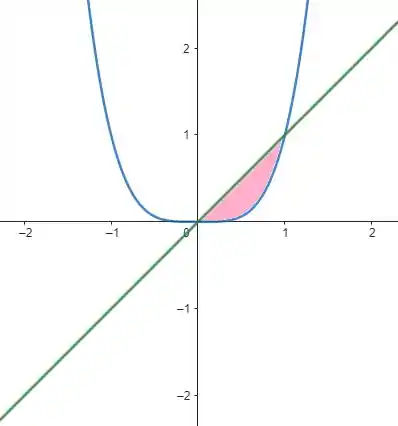
Temos a curva em verde e a curva em azul. A área que queremos calcular está em rosa.
Pra montar a integral, temos funções em função de e a variação é só entre e .
Os limites de integração serão e . E pra achar a área entre as curvas, fazemos a integral da curva que está acima menos a curva que está embaixo. A integral fica:
Passo 3
Calculando essa integral: