Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 321123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UNICAMP – Cálculo 1 – Professor Ricardo Martins – Lista de Integrais

11.8 Seja R a região limitada pelo eixo x e pelo gráfico de y = 1 - 4 x 2 , com x ∈ - 1 2 , 1 2 . Seja S o sólido obtido ao girarmos R em torno do eixo x . Encontre a área de R e o volume de S .

Passo 1

Falaaa... tudo bem??

Nessa questão vamos calcular a área R da região limitada pelo eixo x e pelo gráfico de y = 1 - 4 x 2 entre x = - 1 2 e x = 1 2 . Pra isso usamos integral:

R = ∫ a b f 2 x - f 1 x d x

E vamos calcular o volume dessa região quando giramos em torno do eixo x :

S = ∫ a b π f 2 x 2 - f 1 x 2 d x

Passo 2

Vamos fazer um esboço da região pra ver se a função fica acima ou abaixo do eixo x :

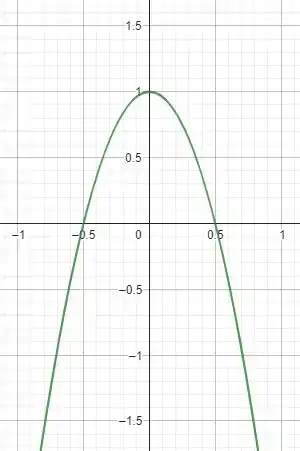
Então a função y = 1 - 4 x 2 está acima do eixo x no intervalo entre x = - 1 2 e x = 1 2

Passo 3

Calculando a área:

R = ∫ a b f 2 x - f 1 x d x

R = ∫ - 1 2 1 2 1 - 4 x 2 - 0 d x

R = ∫ - 1 2 1 2 1 - 4 x 2 d x

R = x - 4 x 3 3 - 1 2 1 2

R = 1 2 - 4 1 2 3 3 - - 1 2 - 4 - 1 2 3 3

R = 2 3

Passo 4

Calculando o volume:

S = ∫ a b π f 2 x 2 - f 1 x 2 d x

S = ∫ - 1 2 1 2 π 1 - 4 x 2 2 - 0 2 d x

S = ∫ - 1 2 1 2 π 1 - 8 x 2 + 16 x 4 d x

S = π x - 8 x 3 3 + 16 x 5 5 - 1 2 1 2

S = π 1 2 - 8 1 2 3 3 + 16 1 2 5 5 - - 1 2 - 8 - 1 2 3 3 + 16 - 1 2 5 5

S = 8 15

Resposta

R = 2 3

S = 8 15

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x