Cálculo de Volume através de Integrais
Seja a região limitada pelos eixos e pelo arco de parábola , para entre e .
a) Calcule a área da região
Passo 1
Vamos começar vendo como fica o gráfico dessa função, temos uma parábola com o coeficiente de negativo. Além disso, as raízes vão ser
A parábola vai ser
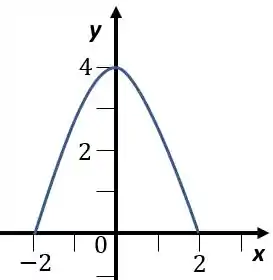
Mas ele só quer de à , então vamos ter
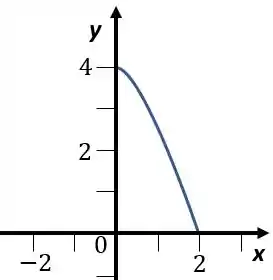
Passo 2
Para acharmos a área vamos fazer a integral dessa função de à
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x