UFRJ – Cálculo 1 – 2020.2 – P4 – Exercício 3
Seja a região limitada do plano que é delimitada pelas curvas:
Sabendo que o gráfico da função , com , divide em duas regiões de área iguais, o valor de é
a)
b)
c)
d)
e)
Passo 1
Fala galerinha, beleza?
Em qualquer problema em que brincamos com áreas entre curvas, o primeiro passo é sempre esboçar as curvas. Em vermelho temos a curva e em azul a curva :
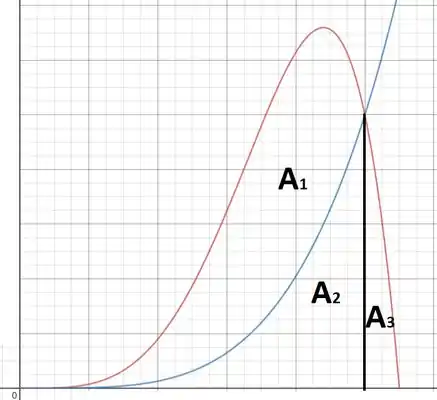
Vale destacar que como não sabemos o valor de , a curva em azul pode cortar a curva em vermelho em qualquer ponto com . Outro detalhe importante: não nos importamos com muitos detalhes sobre a curva vermelha, apenas que ela apresenta raízes em e .
É importante encontrar o ponto de intersecção entre as curvas. Para isso, igualamos
Simplificando dos dois lados:
Passo 2
Para que a curva azul corte a região em duas regiões com áreas iguais, devemos ter
Vamos calcular . Repare que se trata da área entre a curva azul e curva vermelha com entre e :
Logo,
Portanto,
Vamos guardar essa informação!
Passo 3
Observe que a área da região corresponde à área entre o eixo e a curva azul:
Já a área corresponde à área entre o eixo e a curva vermelha com variando de até :
Logo,
Passo 4
Bom, agora a parte de calcula acabou, resta apenas equacionar tudo e achar ! Sabemos que . Substituindo tudo:
Resolver essa equação não parece ser uma coisa muito simples. Vamos fazer o seguinte: passar tudo que envolve para o mesmo lado:
Colocando em evidência:
Portanto,
Ufa, estamos quase lá! Podemos escrever
Tiramos a raiz sexta dos dois lados:
Assim,
Como , o termo dentro do parêntesis deve ser menor que , de modo que escolhemos o sinal de :
Depois desse rolê gigante, chegamos na alternativa C 😉.
Resposta
Alternativa C.