Seja a região plana dada por
a) Esboce a região Indique explicitamente os pontos de interseção entre as curvas.
b) Escreva a área da região através de uma integral na variável
c) Calcule a área da região
Passo 1
Bom, pra começar essa questão, vamos partid o mais fácil. Temos que
Essa dus primeiras são mais ismples, concorda, que seria
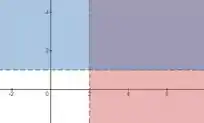
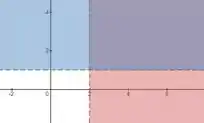
A região em vermelho nos mostra , enquanto a azul nos mostra . Então Agora precisamos ver a outra restrição que temos em , que seria . Ou seja, dessa vez a região vai estar abaixo de .
Observa que temos a função exponencial, como o +1 na frente, o que nos indica que ela está deslocada 1 unidade em direção a y positivo, ou seja
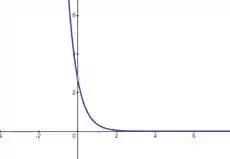
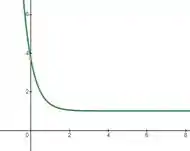
Tranquilo, né? Agora é só juntar tudo!
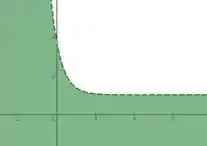

Passo 2
A letra a ainda nos pede para determinarmos os pontos onde as curvas se encontram. Tranquilo! É só sair igualando as funções!
A primeira interseção é entre o e , que é obviamente no ponto . A segunda vai ocorrer entre e
Tranquilo?? Temos então
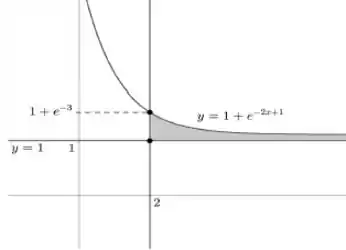
Lindo, né?
Passo 3
Partindo pra letra b) agora, ele só nos pode pra escrever a área através de uma integral certo (na varaável x!! Atenção nisso!!)? Bora lá então.
Se nós fizermos
Isso seríamos nós calculando toda a área abaixo da função (até chegar no , indo de até , ou seja

Para corrigir isso, fazemos então a função menos a função , ficando então

Então nossa integral vai ser
Passo 4
Por último, mas não menos importante, a letra c) nos pede pra calcular essa integral
Por substituição simples temos
Substituindo o pelo valor incial temos
Vamos ter que calcular um limitinho aí
Resposta
