Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 238123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFMG, Sem Campus, Cálculo 3, Listas de Cálculo 3 - UFMG - Lista 1 - Integrais Duplas e Triplas, Questão 23

Seja R a região do plano x y interior ao cardióide x 2 + y 2 = x 2 + y 2 + y e exterior ao círculo x 2 + y 2 = 1 . Calcule:

R = ∬ 1 x 2 + y 2   d A

Passo 1

Eaee!!! Belezinha? Bom... queremos encontrar o resultado da integral:

∬ 1 x 2 + y 2   d A

Onde d A é o diferencial de área.

Em outras palavras, a área que queremos encontrar está mostrada na seguinte figura:

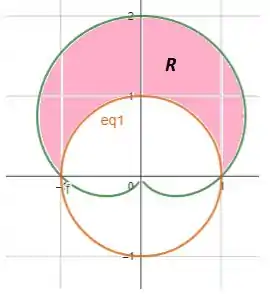
Passo 2

Bom... dessa forma, temos em coordenadas polares:

x = r cos ⁡ θ

y = r   s e n   θ

d A = r   d r   d θ

Passo 3

Agora, vamos encontrar os limites da integração:

  1. Limite inferior:

    2. x 2 + y 2 = 1 ∴

    r cos ⁡ θ 2 + r sen ⁡ θ 2 = 1

    r = 1

  2. Limite superior:

x 2 + y 2 = x 2 + y 2 + y   ∴

r 2 = r + r   s e n   θ ∴

r = 1 + s e n   θ

Passo 4

Agora, integrando, temos:

∫ 0 π ∫ 0 1 + s e n   θ 1 r 2   r   d r   d θ ∴

∫ 0 π ∫ 0 1 + s e n   θ   d r   d θ ∴

∫ 0 π s e n   θ   d θ ∴

= 2

Entendeu direitinho? Responde aee ;)

Resposta

= 2

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x