UFSC, Joinville, Cálculo II, Provas Profº Rómulo Castillo - P2 2015.2, Questão 3b
Sejam as curvas e desenhadas em anexo. Formule, em cada caso, uma integral para calcular:
b) A área exterior à rosa e interior ao círculo .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente calcular a área da região polar dada fora da rosa e dentro do círculo , mostradas no gráfico:
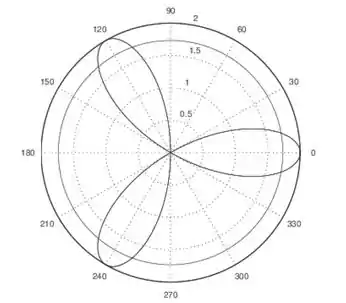
Em coordenadas polares a área entre essas regiões é dada pela integral:
Onde e . Pra descobrir o intervalo , basta igualar as duas curvas pra descobrir onde elas se encontram. Em seguida, substituímos os dados na integral e calculamos a área.
Vamos lá!
Passo 2
Vamos começar igualando as curvas pra encontrar os pontos de interseção:
Assim, ou . E temos:
Integrando nesses intervalo, vamos obter:
Separando os termos, temos:
Nós sabemos resolver a integral da constante , só falta aplicar os intervalos de integração. Mas antes vamos dá uma olhada na integral da esquerda:
Vamos reescrever usando a identidade :
Resolvendo as integrais, temos:
Vamos juntar tudo na nossa integral original:
Aplicando os intervalos de integração:
E temos:
Prontinho, galera! Até a próxima! 😉