Sejam um número real positivo e a região limitada pelas retas e e os eixos e , no primeiro quadrante do plano cartesiano. Sabe-se que a área da região é igual a . O valor de é
Passo 1
Falaaaaa, blz?? Bora começar essa provinha de cálculo, começando com um problema de região entre retas. Para entender o que iremos fazer, bora fazer o desenho do que está ocorrendo para termos um norte?
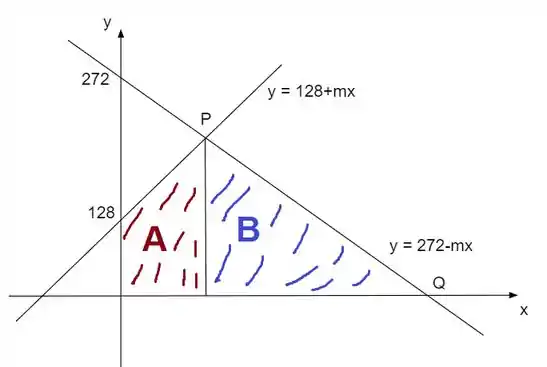
Passo 2
A motivação aqui será abrir a área que mede nas duas áreas , pois são áreas que conseguimos calcular, bora fazer isso.
Primeiro vamos olhar para área A. Essa área é um trapézio, vamos lembrar como é essa fórmula?
Onde:
base menor
B = base maior =
H = altura =
Agora, veja que para calcularmos a base maior e a altura precisamos do ponto P, bora achar ele? Veja que P é o ponto de interseção entre as retas, ou seja, basta igualarmos as equações:
E por isso
E colocando numa equação:
Substituindo
Agora podemos calcular a área do trapézio:
Passo 3
Agora vamos olhar para B:
Veja que B será a área de um triangulo retângulo, ou seja:
A altura acabamos de calcular, que é
A base será:
Onde será a raiz da reta , ou seja:
Por isso, temos que:
Então, temos que:
E então, podemos voltar e calcular .
E por isso, temos que , e acabamos esse probleminha, bora para o próximo??
Resposta
Escrever só a resposta aqui quando o problema tiver resposta