Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Área entre Curvas

Ver Teoria
Exercício 258123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPB, Sem Campus, Cálculo Diferencial e Integral II, Listas de Cálculo 2 - Lista de Exercícios 2, Questão 5

Use o Cálculo para encontrar a área do triângulo cujos vértices são 0,0 ,   3,1 e 1,2 .

Passo 1

Eaee!!! Belezinha? Bom...a questão nos dá três pontos que são os vértices de um triângulo.

Para ficar melhor o que iremos fazer, vamos plotar o triângulo:

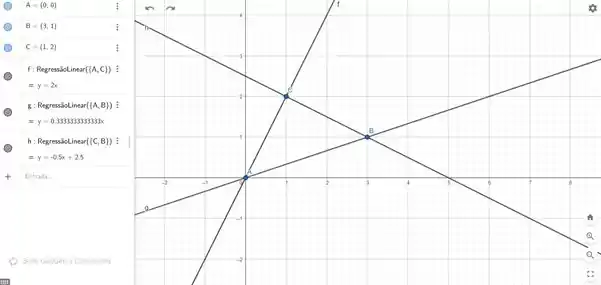
Queremos encontrar a área desse triângulo!!

Uma forma de calcularmos é encontrar a equação de cada reta e aplicar na integral considerando as posições e os pontos de encontro entre as retas.

Lembrando que uma reta é dada pela equação y = a x + b .

Não entendeu? Então bora junto 😉

Passo 2

Bom... fazendo a equação da reta A C :

0 = a * 0 + b ∴ b = 0

2 = a * 1 + b ∴ a = 2

Logo, temos que y = 2 x .

Para a reta C B :

1 = a * 3 + b ∴ b = 2,5

2 = a * 1 + b ∴ a = - 0,5

Logo, temos que y = - 0,5 x + 2,5 .

E, para a reta B A :

1 = a * 3 + b ∴ a = 1 / 3

0 = a * 0 + b ∴ b = 0

Logo, temos que y = x 3 .

Passo 3

Dessa forma, considerando as posições e os pontos de encontro entre as retas, a área do triângulo será:

A = ∫ 0 1 2 x   d x + ∫ 1 3 - 0,5 x + 2,5   d x - ∫ 0 3 x 3   d x ∴

A = x 2 1 0 + - 0,5 x 2 2 + 2,5 x 3 1 - x 2 6 3 0 ∴

A = 2,5

Entendeu direitinho? Responde aee ;)

Resposta

A = 2,5

Exercícios de Livros Relacionados

Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin ⁡ x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x