UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, AV3 - 2022.1
Use a integral dupla para calcular a área da região D limitada pelas curvas
Passo 1
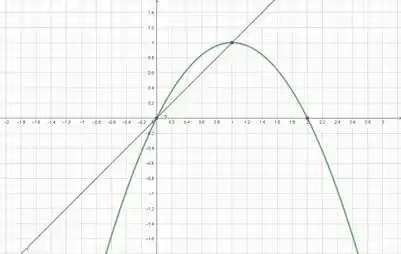
Olá meu amigo, o primeiro passo a ser dado é desenharmos a região que iremos integrar, e para isso usaremos o GeoGebra.
Passo 2
A nossa região de integração está delimitada pela linha verde e pela linha roxa. Agora iremos montar a nossa integral
Passo 3
A segunda integral
Resposta
Exercícios de Livros Relacionados
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = sin x , 0 ≤ x ≤ π
Use um gráfico para dar uma estimativa grosseira da área da região que fica abaixo da curva dada. A seguir, ache a área exata y = x - 4 , 1 ≤ x ≤ 6
Calcule a integral, interpretando-a em termos das áreas. ∫ - 1 3 3 - 2 xd x