UTFPR, Sem Campus, Cálculo Diferencial e Integral 3, AV2 - 2022.1, Questão 5
Calcule o fluxo de sobre a superfície fronteira do sólido delimitado pelo cilindro e os planos e .
Passo 1
Oiie, tudo certinho com você?
Queremos o fluxo do seguinte campo vetorial
o fluxo pode ser traduzido como o cálculo da seguinte integral
a superfície é delimitada pelo cilindro
e os planos e . Ou seja, esse é um cilindro que tem como eixo central! Os valores de vão de a , e podemos usar coordenadas cilíndricas um pouco modificadas para escrever o nosso problema! Saca só!
Passo 2
Normalmente nossos cilindros tem a altura com eixo central , mas, nosso caso temos que o cilindro está deitado e podemos usar as coordenadas cilíndricas com eixo central em , ou seja, da seguinte maneira
em que e , e o elemento de área é agora dado por , que é área de um pequeno retangulozinho na lateral de nosso cilindro. Usando estas coordenadas para escrever nosso campo vetorial, temos que a integral toma a seguinte forma
Vamos calcular os nossos vetores tangentes! Vem comigo!
Passo 3
Temos que os vetores tangentes podem ser obtidos por derivação parcial
e, da mesma forma, temos que
Podemos então obter o vetor normal de nossa integral de superfície, como
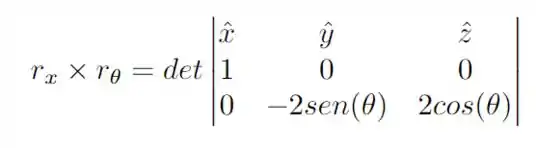
Expandindo o determinante, temos o seguinte vetor
No próximo passo usaremos o vetor obtido para calcular o produto escalar e obter as integrações que precisam ser resolvidas! Bora lá!
Passo 4
Temos o seguinte produto escalar em nosso integrando
Que pode ser expandido como
Substituindo este resultado em nossa integral, temos que
Aqui fica clara a vantagem de utilizar esta escolha de sistema de coordenadas! Note que as variáveis e são independentes e têm limites de integração constantes, portanto, podemos integrar na ordem que bem entendermos. Convenientemente, vou realizar a integral em primeiro! Vem comigo!
Passo 5
O motivo que escolhi realizar a integração em primeiro é porquê
Pois temos que . Como a integral acima é zero, nós economizamos o trabalho de realizar uma integração por partes em . Agora, o trabalho se resume em calcular a seguinte integral
Usando a relação de duplo ângulo para o seno, temos que
Podemos expandir o produto, e obter três integrações
Vamos resolver estas integrais agora! A ideia de como proceder com elas já foi utilizada nos passos anteriores, consegue enxergar? Saca só!
Passo 6
Temos que a primeira integral é bastante direta
a segunda integral é bem similar a uma que resolvemos antes, temos que
já que novamente . Por último, usando a relação de ângulo duplo para o cosseno, temos que
Da mesma forma que fizemos anteriormente, temos que a primeira integral é e a segunda é , portanto, temos que
Ou seja, a integral que queríamos calcular originalmente é
Vamos voltar agora para a nossa integral de fluxo!
Passo 7
Usando o resultado que obtivemos nos passos anteriores, temos que
ou simplesmente
Ou, avaliando os limites de integração, obtemos que
A questão foi isso! Te vejo na próxima! Tchau Tchau!