Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Integrais Duplas sobre Regiões Gerais

Ver Teoria
Exercício 149123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFPE – Cálculo 2 – Listas Prof. Ricardo F. da Silva – Undecima lista – Questão 2a

Calcule as integrais a seguir

a ) ∬ R y 2 d A ,   o n d e   R   é   a   r e g i ã o   d e l i m i t a d a   p o r   y = 0 ,   y = 2 x + 4 ,   y = x 3

Passo 1

Oi, tudo bem? Vou te ajudar a resolver essa questão! Vamos lá?

O problema nos deu essa integral dupla

∬ R y 2 d A

E a região:

y = 0

y = 2 x + 4

y = x 3

E pediu para calcular isso! Mas qual é o pulo do gato?

É descobrir que região estamos integrando e os limites de integração! Vamos esboçar nossa região

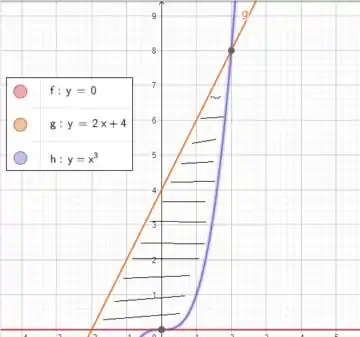Vemos que à direita sempre está a curva roxa, enquanto à esquerda sempre está a curva laranja! Isso significa que nossa ordem de integração será

d x   d y

E os limites

y - 4 2 ≤ x ≤ y 3

0 ≤ y ≤ 8

Beleza? Agora é só montar a integral e #partiu resolver!

Mas relaxa, vou fazer junto com você!

Passo 2

Agora vamos montar a integral! Nossa integral é

∬ R y 2 d A

Os limites de integração

y - 4 2 ≤ x ≤ y 3

0 ≤ y ≤ 8

E o diferencial de área

d A = d x   d y

Agora vamos juntar

∫ 0 8 ∫ y - 4 2 y 3 y 2   d x d y

Tudo bem até aqui?

Passo 3

Agora é #partiu resolver, primeiro em x :

∫ 0 8 ∫ y - 4 2 y 3 y 2   d x d y

= ∫ 0 8 y 2 x y - 4 2 y 3   d y   = ∫ 0 8 y 7 / 3 - y 3 2 + 2 y 2   d y

Beleza? Agora vamos integrar em y :

= 3 10 y 10 / 3 - y 4 8 + 2 y 3 3

E aplicar os limites de integração

= 3 10 2 10 - 8 4 8 + 2.8 3 3 = 3072 10 - 512 + 1024 3

E por fim simplificar

9216 - 15360 + 10240 30 = 4096 30 = 2048 15

Pronto! Essa é nossa resposta!

Beleza? Espero ter ajudado!

Resposta

2048 15

Exercícios de Livros Relacionados

Determine o volume do sólido dado.Limitado pelos planos x = 0 , y = 0 , z = 0 e x + y + z = 1
Determine o volume do sólido dado.Abaixo do paraboloide z = 3 x 2 + y 2 e acima da região delimitada por y = x e x = y 2 - y .
Calcule as integrais iteradas.int_0^1 int_(x^2)^x ( 1 + 2 y ) d y d x
Calcule a integral dupla. ∬ Dy 2 e x y d A, D = x ,y0 ≤ y ≤ 4,0 ≤ x ≤ y }
Calcule as integrais iteradas. ∫ 0 1 ∫ 0 x 2 ( x + 2 y ) d y d x