PUCRIO - (Cálculo 2 - MAT1162) - G2 (Versão A) 2020.1
Considere uma lâmina que ocupa a região planar que se encontra entre as curvas , e . Suponha que a densidade em um ponto qualquer na lâmina seja dada pela função . Determine a massa total da lâmina.
Passo 1
Galera, bora lá! Pra início de conversa, tamos falando de várias curvas no plano e acho que fica confuso trabalhar com elas todas sem um esboço. Veja que pras curvas exponenciais, quando , teremos os seguintes valores de :
E que essas curvas vão se interceptar no seguinte valor de :
Um bom esboço então será:
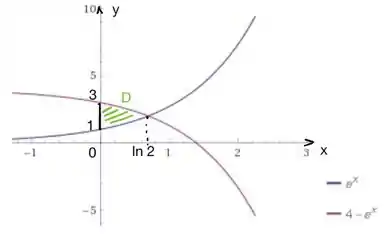
Sendo que a lâmina, como o próprio enunciado disse, é a região entre essas curvas. Pra calcular a massa total, é bem aplicação de fórmula mesmo galera! Afinal temos uma equação lindíssima ela a partir da densidade:
A gente pode abrir essa integral já e por os limites de integração direitinho. Afinal, sabemos que:
E do nosso esboço, vemos que a região de integração , que define a lâmina, vale:
Show de bola!! Sendo, do enunciado mesmo, , nossa massa fica:
Nos próximos passos, o que faremos é resolver essas integrais!
Passo 2
Show, vamos começar com a integral de dentro:
Essa integral esnobe quer nem saber quem é , afinal ela tá em função de . Vamos tratar que nem uma constante então, e a integração vira a de um polinômio de do primeiro grau, resultando em:
Simplificando, temos:
Passo 3
Agora a gente coloca esse resultado dentro da integral dupla que tínhamos antes:
E integramos em relação a ! Pra isso eu já dou um adianto aqui: a maior parte das vezes que temos um produto de funções diferentes na integral, ela sai por integração por partes. Uma boa forma de eliminarmos esse multiplicando é considerarmos:
Onde:
Sendo a integração por partes um método onde vale:
Derivamos e integramos , achando:
E logo, temos:
O que simplificando, resulta em:
A única coisa que falta é aplicar os limites de integração! Mãos a obra!
Levando em consideração que é uma propriedade das exponenciais, chegamos a:
E ta na mão! Achamos a massa total!