Integral dupla sobre regiões mais gerais
Considere as regiões planas
Seja
- Esboce a região e identifique sua fronteira como uma curva clássica (ou seja, forneça seu nome e sua equação)
- Esboce o interior da região e determine-o através de desigualdades.
- Esboce a região e identifique sua fronteira como uma curva clássica (ou seja, forneça seu nome e sua equação)
- Esboce a região e, em seguida, descreva-a no seguinte formato:
Explicitando as constantes reais e e as funções e .
Passo 1
A região é uma circunferência lembra? A fórmula geral de uma circunferência é
Nesse caso
O seu gráfico fica
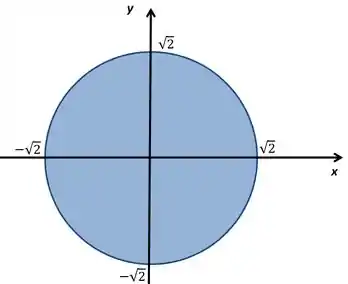
Passo 2
Repara que agora ele quer todos os pontos que e são maiores ou iguais a . A parte de dentro vai ser aquela que não tem o igual, ou seja,
E seu gráfico vai ser pintar o primeiro quadrante do plano cartesiano
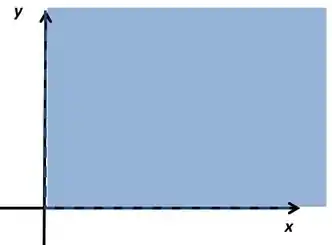
Precisa desse tracejado porque ele não está incluindo quando temos ou
Passo 3
Isso é uma parábola, só que ela está com o eixo de simetria no eixo , ela está tortinha tá vendo?
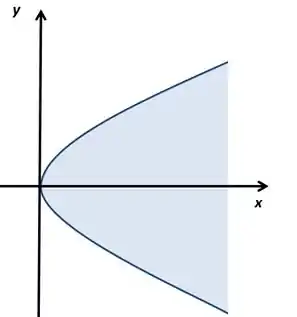
Passo 4
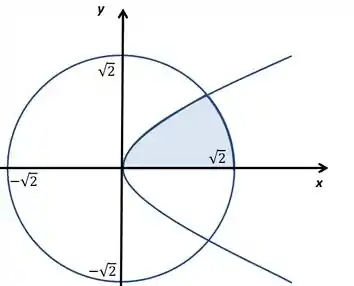
Vamos agora fazer essa zona toda junta
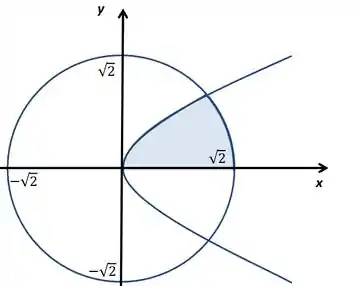
Se quisermos escrever da forma que ele disse podemos ver que o valor de vai de até o seu valor quando a circunferência e a parábola se cortam. Vamos calcular esse ponto substituindo o valor de na circunferência.
Colocando isso na circunferência
Como podemos ver o único que serve é o
Então o valor de que eles se encontram é
Porque o , então temos
Passo 5
Vamos agora aos limites de , pela figura o valor de vai da parábola à circunferência.
Então ele vai de
Até
Repara que peguei o positivo porque estamos pegando valores de
Então
Então
Resposta
-
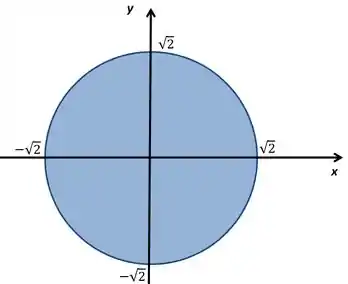Circunferência -
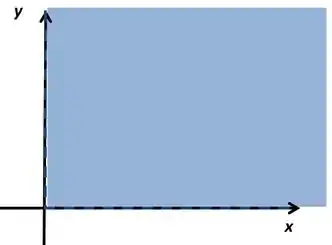
x , y ∈ R 2 x > 0 , y > 0 -
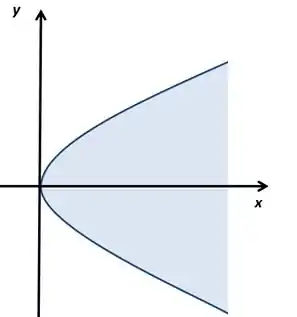parábola 