Determine o valor da integral dupla
Para o qual é o interior de um quadrado cujos vértices estão sobre os eixos coordenados
Passo 1
Essa questão parece que está faltando alguma informação, não é? Ele não fala muito sobre o quadrado, ta bem estranha. Enfim, na prova não vamos deixar em branco, né? Vamos dar um tamanho qualquer para o lado do quadrado e resolver isso.
O enunciado diz que os vértices do quadrado estão nos eixos coordenados, então um esboço é esse aqui
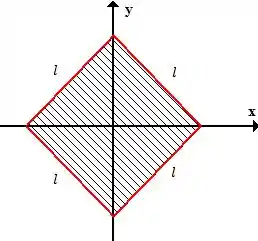
A gente poderia até tentar resolver essa integral bizarra aí que o enunciado deu, ia dar um trabalho surreal e podíamos errar contas muito fácil. Não vamos fazer isso dessa vez, tem um macete aqui que vai salvar nossa vida!
Existe um conceito no cálculo que é o de função ímpar, uma função ímpar matematicamente é definida por
Mas como assim?
Calma, isso é meio teórico demais mesmo, vou dar um exemplo simples:
Quando fizemos a função de o resultado deu exatamente inverso de , logo essa função é ímpar!
O mesmo não acontece com a função
No caso essa função não é ímpar, sacou a diferença?
Ta, mas pra que estou lendo isso, responde aí? Como me ajuda na questão?
Existe uma definição que diz que, se integrarmos uma função ímpar em uma região simétrica em relação à origem, o resultado da integral é zero!
Passo 2
Beleza, o conceito de função ímpar entendemos, mas que bruxaria é essa de “região simétrica em relação à origem???
Me acompanha aqui, imagina só metade do quadrado, mais especificamente a metade de cima
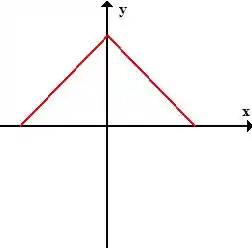
Se usarmos a origem como espelho pra cada ponto dessa curva vermelha aí, olha o que encontramos
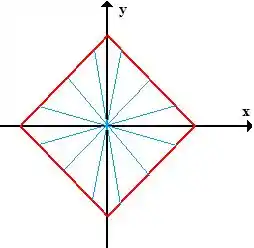
Ou seja, o quadrado que é a nossa região de integração é totalmente simétrico em relação à origem!
Passo 3
Só precisamos provar agora que a nossa função que vamos integrar é ímpar que o resultado da integral vai ser zero!
Vamos analisar nossa função então
Portanto a função é impar!
Passo 4
Provando que a função é ímpar (Passo 3) e que o intervalo de integração é simétrico em relação à origem (Passo 2), podemos afirmar que