Determine o volume do sólido limitado pelos planos coordenados e pelo plano .
Passo 1
Fala turminha, tudo em cima? Bora lá resolver essa questão. Sem mistério, precisamos desenhar o plano que ele descreve na questão. Apresentando uma forminha 3D pra gente visualizar melhor:
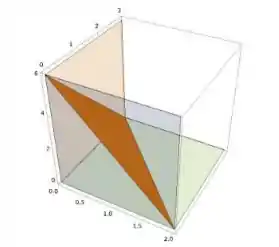
O nosso sólido é do formato de uma pirâmide de base triangular.
E para encontrar o volume dessa pirâmide, usaremos uma integral dupla do tipo:
Agora precisamos saber quem é e quem é a região de integração .
Passo 2
Para encontrar basta isolarmos a variável na equação no plano dada pelo problema. Assim:
Então
E encontramos
Essa será a função que iremos integrar. Agora nos resta determinar a região de integração.
Passo 3
Observar o seguinte: Olhando pelo eixo do sólido,
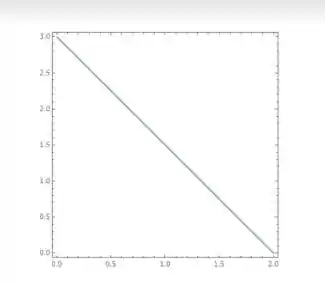
A região formada por valores de e
Assim, nossa integral será uma integral dupla em que os valores de estão variando entre constantes indo de até e os valores de então variando desde até a função .
Mas ainda não sabemos qual é essa função , por isso devemos determina-la antes de partir para a integração.
Perceba que a função tem como gráfico uma reta, então sua lei de formação é dada por
E existem dois pontos no gráfico que conseguimos utilizar para encontras os valores de e . Os pontos são e (2,0).
Substituindo esses pontos na lei de formação ficamos com o seguinte sistema:
Sendo , podemos substituir na primeira equação e encontrar
E nossa função então será dada por
E assim podemos voltar a discussão sobre os limites de integração.
Assim, nossa integral será uma integral dupla em que os valores de estão variando entre constantes indo de até e os valores de então variando desde até a função .
Ou seja
E nossa missão agora será desenvolver essa integração aí.
Passo 4
Usando o Teorema de Fubini iremos integrar primeiro a integral de dentro que está em , assim, a variável será vista como uma constante.
E finalmente, é isso! Se você gostou, ou ainda ficou alguma dúvida na questão, dá um feedback pra gente! Vamos adorar te responder