UNICAMP – Sem campus – Cálculo 2 – P2 – 2022.1- 5
Determine o volume do sólido limitado pelos planos coordenados e pelo plano .
Passo 1
Fala turminha, tudo em cima? Bora lá resolver essa questão. Sem mistério, precisamos desenhar o plano que ele descreve na questão. Apresentando uma forminha 3D pra gente visualizar melhor:
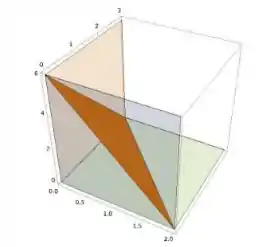
O nosso sólido é do formato de uma pirâmide de base triangular. Mas, vamos observar o seguinte: Olhando pelo eixo do sólido,
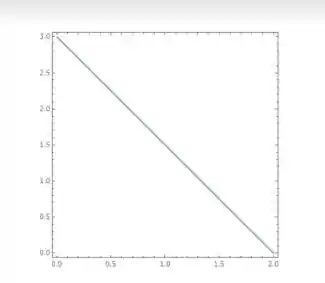
É uma região D formata por , e (para )
Passo 2
Beleza, é justo você estar se perguntando porque essa informação é útil... ? pois bem. Com isso, podemos montar nossa integral tripla para volume usando as retas que limitam a região D. Ou seja, montando a integral, temos (de x, para y, para z):
X limitado por e .
Y limitado por 0 e
Z limitado por e 0. Dessa forma:
Agora o desafio é resolver a integral!
Passo 3
Bem, resolvendo-a:
Primeiro para . Aqui fica tranquilo pois o integrador é 1, então a integral já fica na forma:
Resolvendo para , aplicaremos a integral:
E por fim resolvendo a última integral:
E é isso! Se você gostou, ou ainda ficou alguma dúvida na questão, dá um feedback pra gente! Vamos adorar te responder