Encontre a área da região limitada pela parábola e pela reta utilizando integral dupla.
(a)
(b)
(c)
(d)
(e)
Passo 1
Nesse tipo de questão, especialmente quando as funções são bem simples de desenhar, é uma boa ideia fazer um esboço:
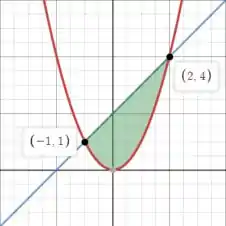
E nosso objetivo é usar uma integral dupla para calcular essa área verde. O programa já mostrou quais são os pontos de interseção, mas precisamos saber calculá-los por conta própria!
Passo 2
Ok, vamos achar os pontos onde as funções se intersectam:
Começamos igualando as duas:
E se reescrevermos isso na forma “fatorada” fica fácil encontrar as raízes:
Beleza, agora já estamos prontos para calcular a área.
Passo 3
Vamos montar a integral.
Olhe para a figura e pense assim: para cada valor de , nós vamos andar (na vertical) de até , e vamos pegar todos os valores de entre e . Matematicamente, escrevemos isso assim:
Resolvendo isso:
E a área da região é:
Resposta
A área da região é (Letra e)