UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 2b.
2 - Esboce a região de integração e calcule as integrais iteradas a seguir
b)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Temos uma função dada por e temos que calcular a integral dupla pra variando de e e depois pra de a .
Só de ver essa função já dá um sustinho, não é?
O que vamos fazer é integrar a função em relação a , depois de integrado vamos aplicar os limites de integração.
A partir do resultado vamos fazer o mesmo com relação a .
Preparado? Bora lá!
Passo 2
Primeiro vamos integrar a função com relação a
Antes, vamos manipular essa função para facilitar nossos cálculos.
Podemos escrever
Assim podemos usar o método de substituição para substituir por
Ainda não acabou, podemos também fazer o seguinte
Agora sim, aplicando o método da soma, temos
Agora temos condições de calcular as integrais
Passo 3
Para a primeira integral, pelo teorema fundamental do cálculo, sabemos que
Para a segunda integral podemos obtê-la facilmente como
Com isso, temos
Voltando para
Aplicando os limites de integração, temos
Tranquilo até aqui?
Passo 4
Agora vamos integrar com relação a
Como a integral da soma é a soma das integrais, logo
Calculando a primeira integral
Por integral de substituição e , logo
Como sabemos, a integral do é igual a
Substituindo por de volta
Aplicando os limites de integração.
Organizando a resposta, temos
Trabalhoso, não é? Mas relaxa, estamos acabando
Passo 5
A segunda integral dada por
Como não temos para integrar, consideramos tudo como uma constante. E qual a integral de uma constante?
Aplicando os limites de integração, temos
Por último, a terceira integral
Como calculamos anteriormente, a integral de é dado por
Aplicando os limites de integração
Passo 6
Substituindo esses resultados, temos
Organizando os resultados, vamos obter
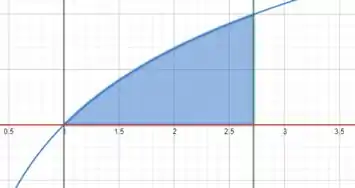
Acabamos?? Ainda não, falta uma coisinha pequena. Vamos esboçar a área de integração
Pelos limites de integração, varia entre e , já varia entre e . A área formada pela intersecção desses intervalos, é
Fim! Iae, o que achou? Responde Aí! 😁
