UFABC. Cálculo. Funções de Várias Variáveis. Lista 6 - Integrais Duplas. Questão 2c.
2 - Esboce a região de integração e calcule as integrais iteradas a seguir
c)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Essa questão foi bem direta com a gente. Temos que visualizar e desenhar a região em que estamos integrando e obter o resultado dessa integral.
Sabe como fazemos pra visualizar o intervalo de integração. Observando a integral, temos
As integrais são dispostas entre as cores que destacamos, ou também os meios e os extremos.
Isso significa que como a integral de é dada pelo limite inferior e o limite superior , nosso está variando entre as curvas e .
Seguindo essa mesma ideia podemos afirmar que está variando entre as curvas e .
Uma técnica pra visualizarmos a área de integração, é hachurar a área entre as curvas de e de separadamente, a área em que a hachura está em comum (para e ) é nossa área de integração.
Entendeu?
Passo 2
Se plotarmos as curvas e obter a área hachurada em comum, vamos ter
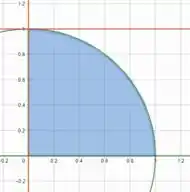
Essa é a nossa região de integração!
Agora vamos calcular essa integral. Primeiro vamos integrar com relação a e depois aplicamos os limites de integração.
Por integral de polinômios, fazemos a divisão entre a variável e a potência e somamos no seu expoente
Aplicando os limites de integração como
Bacana, não é?
Passo 3
Agora a partir desse resultado, vamos obter a integral com relação a
Podemos tirar a constante para fora da integral e aplicar o método da soma
Sabemos que a integral de uma constante é a própria constante multiplicada pela variável e a integral de é obtida pela integração de polinômios.
Substituindo na integral anterior e aplicando os limites de integração, temos
Organizando nosso resultado, vamos ter
É isso! Essa resolução te ajudou? Responde Aí! ✌
