UFPE, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº Ricardo F. da Silva - Undécima Lista, Questão 3a
Esboce a região de integração e calcule a integral trocando a ordem de integração.
a)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente trocar a ordem de integração, esboçar a região e calcular a integral. Essa região de integração é definida pelos intervalos da integral dupla que ele nos deu. Nesse caso, temos a região:
Repare que tanto quanto vai de a , nesse caso. Esboçando a região, temos:
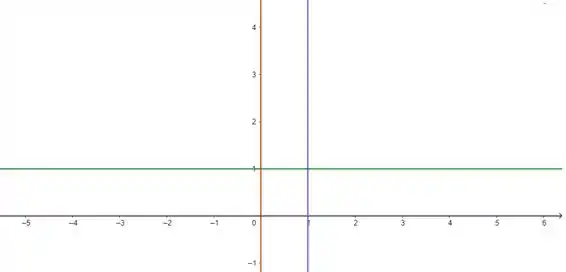
A reta laranja representa , a reta em roxa representa e as retas em cinza e em verde representam e , respectivamente. Agora vamos trocar a ordem a integração e calcular a integral.
Vamos lá!
Passo 2
Como os intervalos são iguais, na prática o que vai mudar é somente a ordem de integração mesmo, os intervalos vão permanecer os mesmos. Assim, vamos ter:
Então, integrando primeiro em relação a , consideramos constante e temos:
Aplicando os intervalos de integração:
E caímos novamente na integral anterior. Essa integral não possui solução pelos métodos convencionais, sua solução pode envolver a expansão em série de potência ou a utilização de métodos numérios e sua solução é conhecida como função de erro imaginário.
Valeu, galera! Até a próxima! 😉