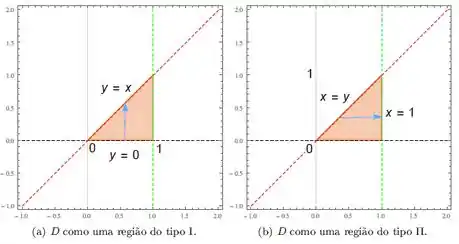
Esboce a região como uma região do tipo e do tipo . Escreva as integrais possíveis e use uma delas para resolver
Onde é limitada pelas retas , e
Passo 1
A questão pede pra gente escrever a região nos dois tipos, certo? Antes disso, vamos ver um esboço do que estamos tratando, sem pensar em tipo nenhum
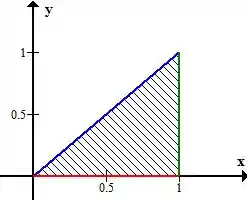
Ta beleza, o esboço é esse aí, onde a reta azul é , a reta vermelha é e a reta verde é .
O que precisamos ver agora é a diferença entra as regiões do tipo e do tipo . No primeiro caso, varia em funções de , ou seja
É como se tentássemos olhar a região de baixo pra cima! Com sendo limitado por .
No caso do tipo , tem uma sutil diferença, é quem é limitado por funções de , assim olha
É como se tentássemos olhar a região da esquerda para a direita!
Olha essa imagem aqui se não ajuda
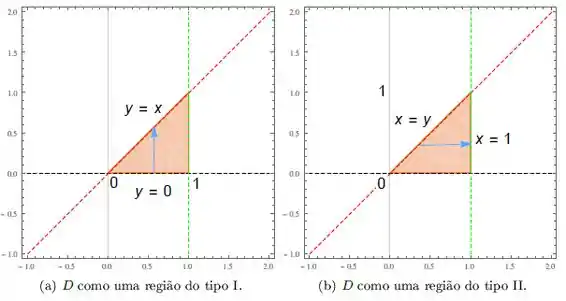
Passo 2
Ah, beleza então, agora é só escrever as regiões! Vamos começar pela do tipo ...
Vemos que na primeira imagem, é limitado em baixo por e em cima por , portanto
Pronto, estão definidos os limites das funções! Agora é só entre que valores - isso mesmo, constantes! – nas quais varia.
Nesse caso ele vai de a , portanto
Passo 3
Vamos agora para a região do tipo
Vemos na segunda imagem que a região é limitada na esquerda por e na direita por , portanto
Agora é a mesma ideia, só ver entre que valores varia.
Nesse caso ele vai de a também, mas nem sempre é assim, toma cuidado!
Pronto! Estão definidas as regiões =D
Passo 4
Agora temos que escrever as integrais possíveis! Vamos ficar com o seguinte:
Vamos resolver a segunda:
Resposta