Sendo a região plana delimitada pelas curvas dadas pela equação e , calcule
Passo 1
Opa, aqui temos uma região descrita pela seguinte integral:
Ela é delimitada por:
Pra facilitar a vida da gente, é legal a gente começar entendendo que região é essa que estamos trabalhando.
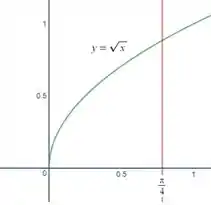
Bom, só com isso a gente já tá com um bom caminho andando! Agora vamos descrever essa região que a gente tá vendo. Se você for observador, nosso varia de zero até , e nosso varia de zero até a função que está em cima, que é . Show, então vamos escrever isso na integral.
Passo 2
Agora vamos resolver essa integral! Começando pela integral de dentro:
Aqui o é uma constante! Vamos usar a substituição:
Substituindo:
Agora precisamos adequar o limite de integração, começando pelo limite superior e depois o inferior:
Então temos:
Ficamos então com:
Passo 3
Agora vamos para a integral de fora:
Integrando:
Então:
Prontinho!